| Application to the electric models
Exact analytical solutions obtained for mechanical elastic lines can be easy extended to electric ladder filters, transmission lines, networks and other systems of such type. For it we have refined the conventional electromechanical analogy. For example, Skudrzyk [17] was successful in this quite effective way. He used it even not refining the analogy system in order to represent the vibration pattern in a mechanical line with complex resonances, but using the conventional solutions for simple electric filters. The necessity to refine the analogy relationship arose, because in the conventional analogy system we see a tendency (see, e.g., [41, pp.88 – 89], [42, pp.32 – 36], [43, pp.12 – 15], [44, pp.408 – 409] or [45, pp.11 – 15]) to establish the correspondence not between the processes in the studied system as a whole, but between the specific elements and their behaviour, irrespective to the compared models. It is accepted that “the main characteristic of the analogy is … the circumstance that to each dependent variable and all derivatives of one system (i.e., x, dx/dt, d2x/dt2) some variable with the same derivatives (q, dq/dt, d2q/dt2) corresponds, and these functions are interconnected so that if some function was known in one system, the corresponding function of the second system can be found. This correspondence just means the analogy” [41, pp.88 – 89]. As a consequence of such approach, to each type of filter, its own mechanical diagram-analogue (see, e.g., [44, pp.426 – 427] or [45, pp.103 – 112]) corresponds, and the system of electromechanical analogy is reduced to two dual between each other correspondences f ~ u and f ~ i. The construction of the analogue circuit is reduced to an elementary operation of elements replacement. “For it one needs:
We changed a little the conventional approach to the electromechanical correspondence establishing and connected into the correspondence not specific elements of the circuits-analogues, but some complexes, or block-diagrams. Rather, we have connected the mechanical and electric models as the whole, grounding on the correspondence of modelling systems of algebraic equations obtained from those differential after eliminating the time dependence. This allowed us to be not so rigidly limited by the correspondence of the specific circuit elements and not to limit the scope of analogues by the differentiation or integration the modelling differential equations. As the result, with the new correspondence of models, the vibration pattern in the circuits has basically changed, retaining the relationship between the models, because the basic principles became more general in choosing the analogues. These principles are connected with the boundary conditions, with the features of a mechanical elastic line as a whole, but the main, with the correspondence of the modelling systems of algebraic equations. Namely the systems of algebraic equations, not one differential equation of the electric circuit on whose basis the relationship of analogy was established up to now (see, e.g., [41, p.89] or [42, pp.32 – 34]). The possibility to introduce such analogy was indicated by Atkinson in [27, pp.32 – 33]. But the matrix methods he used to obtain the solutions for a mechanical system enabled him neither to develop this direction nor to exceed the frames of simplest LC and CL ladder filters, nor write in general form the relationship of correspondence between the compared systems, nor to obtain analytically the solutions themselves. We have reported about our analogy relationship at the international conference “Control of Oscillations and Chaos” (Saint-Petersburg, July 2000) [46]. Furthermore, the necessity to change the electromechanical analogy was caused by the original approach to solving the problems of mechanical long lines; we intended to use them to investigate the vibrations in ladder filters. With the changing approach to the mechanical model solution, there passed the necessity to consider a ladder filter as a simple assemblage of particular two-ports – i.e., to use the conventional approach applied, for example, in [41, pp.351 – 355], [44, pp.408 – 410] or [45, p.102] to find the analogy between the long line and ladder filter. Note that the electromechanical analogy limitedness by the specific two-ports seen in the literature is conditioned mainly by the practice of ladder filters calculation by the two-port method. It is conventional that “one of the two-port method advantages is that the complicated circuit can be reduced to the composition of a few simple two-ports. The coefficients of each can be easily expressed through the elements parameters of the circuit corresponding sections. And the connection of several two-ports can be presented in its turn as some resulting two-port. The matrix coefficients finding is mainly reduced to the summing and multiplying the matrixes of separate two-ports to which the considered circuit was decomposed” [10, p.53]. Actually, the two-port method much simplifies the calculation. However the investigations we have carried out proved that for ladder filters the correspondence with mechanical analogues based on the modelling system of algebraic equations is true. This extends and generalises the concept of electromechanical analogy and allows to introduce a whole class of ladder filters for each mechanical model. By the example of the specific semi-finite homogeneous ladder filter we have proved that the solutions obtained by the two-port method are set to the matched ladder filters. And even in this case the filter wave properties ignored by the two-port method lead to the inexact determination of the input impedance phase characteristics. As the calculations done with the help of our Dynamical Electromechanical Analogy (DEMA) show [49], in the filter pass band the input impedance has a complex phase increasing with the growing frequency as arc sine. With it the filter characteristic impedance cannot be determined as the product of impedances of ladder filters with shorted and opened ends. In these regimes the mismatch of the filter output impedance and the load takes place and a standing wave produces, and the input impedance depends nonlinearly on the number of filter sections and on the external excitation frequency. The solutions obtained by DEMA enable to take into account the wave properties of a ladder filter. This conditions their exactness and completeness comparing with the known solutions obtained by the two-port method. Besides, this complex of solutions is much more visual at all stages of investigation and is structurally determined. This is essential when synthesising the ladder filters with given characteristics. These solutions can be extended to the branching circuits of the filters having a complicated topological structure. This opens a new scope in synthesis of the filters with given parameters, as well as in the electrophysical modelling in the complex periodical structures. |
|
|
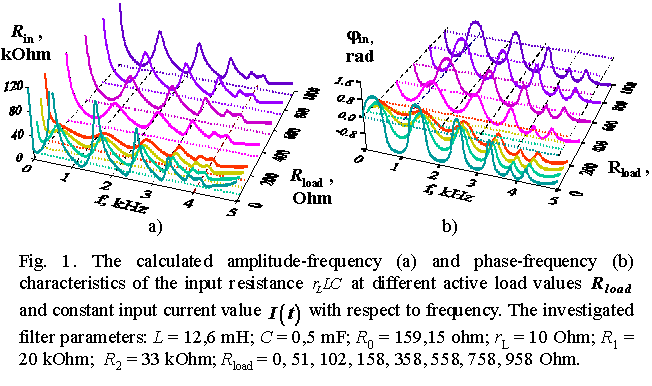
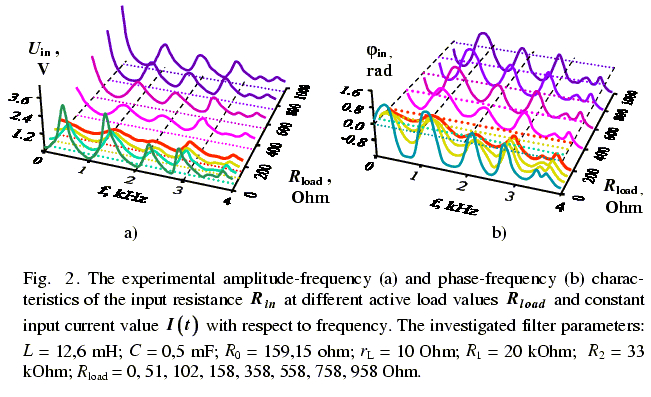
To verify the new calculation method, we have set up a 6-sectioned mismatched ladder filter and taped off its characteristics experimentally. As one can see in presented Figures 1 and 2, the coincidence between the experimental characteristics and those calculated by our method is up to small shades conventionally thought to be the experimental noise. The full report of this investigation is available here. |
|
Proposal |
|
State of the art |
|
The
main results of our method in brief |
|
Applications to the
mechanics, acoustics and geophysics |
|
Applications to the mismatched
ladder filters, transmission lines and networks |
|