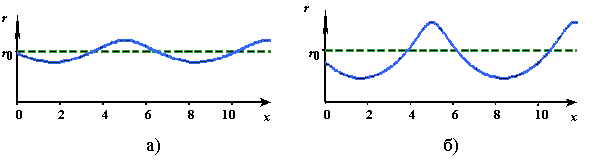|
Applications
to the mechanical models, acoustics and geophysics Although our method is young, its applicability to the
widest range of practical investigations is already obvious. It can be easy
extended to the torsion vibrations; instead the longitudinal and transversal
co-ordinates one can introduce those generalised; and so on. Even not
transiting to the spatial problems, these solutions can be applied to 1D
processes in elastic rods. In Fig. 14 we show the pattern of transversal
vibrations in a semi-finite rod, which accompany those longitudinal and
propagate along the rod lateral surface. However these waves are not Rayleigh
waves, though the production of these last is caused also by the material
transversal deformation under longitudinal vibrations. Their propagation
velocity is equal to that of longitudinal waves and is not determined by
Poisson coefficient, as Rayleigh waves are. The more, we can prove that if
the propagation velocity of transversal waves accompanying the longitudinal
waves differed from these last, then in the elastic line there occurs a
paradoxical phenomenon: in the region of rod local tension its cross-section
increases, and with compression it tapers. |
|
|
|
|
|
Fig. 14. General
form of the transversal surface wave propagating in a semi-finite elastic rod
having finite cross-section, under the longitudinal dynamical load on the
free end of the rod whose value is 0,2 of that critical (a) and 0,5 of
critical (b) |
|
|
|
|
|
In the presented
plots one can see one more feature of this process. At small external force
amplitudes the surface waves are practically sinusoidal, and it can be
corroborated mathematically. With the growing external force amplitude the
wave deforms, and at its definite value in the region of dynamical
compression the rod breakage occurs (the vibration amplitude turns into
infinity). With it we investigated all vibration pattern transformations in
frames of linear modelling, but with the help of our complete, determined,
non-matrix analytical solutions. |
|
|
|
|
|
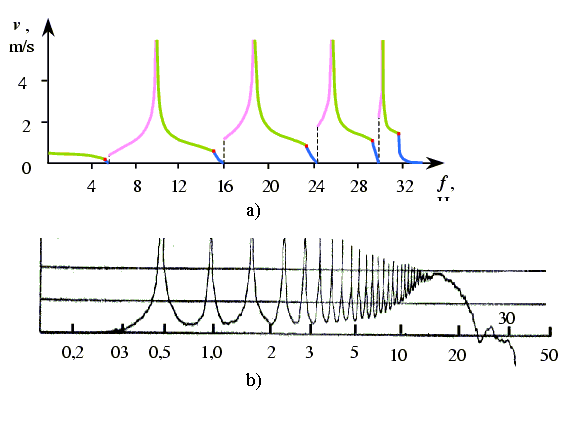
Fig. 15. The amplitude-frequency
characteristic of vibration velocity of the first element of a semi-finite
elastic line having the resonance subsystems (a) and the experimental
regularity for the longitudinal wave propagation velocity in a polyethylene
rod as a function of frequency (b) |
|
|
|
|
|
In Fig. 15 [50] we show two
plots. In the left plot one can see the amplitude-frequency characteristic
for an elastic system having the resonance subsystems obtained by our method,
and in the right plot � the experimental data by Skudrzyk [17, p.244]. With
the exception that the solutions did not take into account the line
resistance, while the experimental data were obtained on the material having
a resistance, the form of resonance peaks coincides. The difference is only
in the splashes at the bottom of the left plot which correspond to the
aperiodical vibration regime and, as we already know, will smooth with the
growing resistance. As to vibration systems having the resonance
subsystems, we underline again an important aspect that the resonances in
these models arise just at the border between the critical frequency for the
system as a whole and that for the subsystem. The answer to this question
consists of a whole complex of answers to many questions of the science and
practice. For example, an atom also is a vibration system having the
resonance subsystems. And an orbiting electron does not radiate, but when
transiting into another orbit at the subcritical frequency, it radiates. We
can present alike instants in more practical areas, such as mechanical,
turbine or aircraft engineering. Aren�t there reflected the errors by the
engineers designing the mechanisms loaded by high-frequency vibrations? One
knows, the problems of conventional methods arise just on high frequencies
near the critical frequency. |
|
|
|
|
|
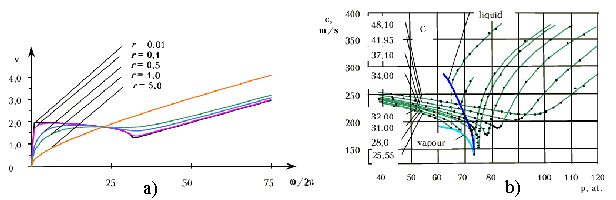
Fig. 16. The
phase velocity of wave propagation vp in a resistant
elastic line as a function of frequency (a) and the experimental data for the
propagation velocity c of ultrasonic vibrations as a function of pressure
p in the vicinity of gas � vapour critical point for the carbonic acid
gas (b) |
|
|
|
|
|
In Fig. 16 [48] we show two
plots in the acoustic area. In the left plot we present again the regularity
of phase velocity of the wave propagation in a resistant elastic line. In the
right plot we show the experimental result on the ultrasonic vibration
propagation in the carbonic acid gas near the vapour/gas critical point
against the pressure and temperature after [23, p.45].
Comparing the obtained theoretical results with the experimental regularity,
we see that their patterns completely coincide. The growing velocity in Fig.
16b and the minimums smoothing, the same as the minimums displacement with
the growing temperature, are fully described by the pattern of the parameters
variation in the analytical regularities on whose basis Fig. 16b has been
plotted. Each regularitiy c(p) in Fig. 16b has its typical
minimum at the critical frequency. With growing temperature this minimum
displaces towards the higher pressure (or higher frequency), and the
sharpness of minimum smoothes because of line resistance growing. At the same
time the wave propagation velocity increases because of intermolecular
distance increasing. Speaking of application of the solutions obtained by
the non-matrix method, we would like to mention briefly the geophysical
investigations. It is commonly known that �almost all seismic zones � are
located on the geosynclines and are inherent in them� [39, p.303], and
�the earthquakes epicentres are located along the largest cracks, or these
cracks are the epicentres themselves. In the tablelands the seismic phenomena
are much uncommon� The cracks related to the kinks of wreath-likely placed
folded mountains are especially liable to the earthquakes, and this
coincidence is specifically inherent in tertiary mountain ranges surrounding
Asia. More often than elsewhere on the Earth the seismic motions reveal in
the Japan Great Graben. Almost all Indian earthquakes are concentrated in the
corners where the Himalayan Arc meets that Iranian from one side and the
Malay from another. Unfortunately, the sufficient attention still was not
given to the close relation between the lines of folds meeting and the shock
lines. But this dependence is observed in the ancient folded areas� [39,
pp.301 � 303]. Even �the degree of shores seismic ability corresponds to the
degree of steepness of their slopes� [39, p.304]. Noting that in most of
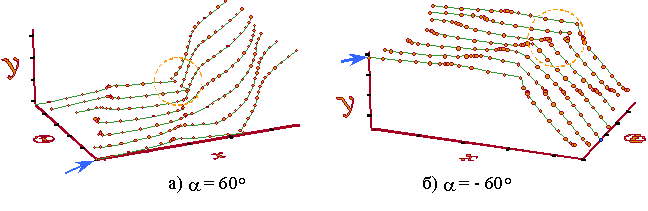
rocks the transversal stiffness relates to that longitudinal as 1,5 � 2 [40, pp. 56 � 61],
it is sufficient to see Fig. 17 (the copy of Fig. 12 of The main results of our method in brief made here for
your convenience) to grasp the reason of this phenomenon. |
|
|
|
|
|
Fig. 17. The
typical vibration diagrams in a homogeneous elastic line with the positive (a)
and negative (b) kink angles under the inclined external force action and
with the inequal longitudinal and transversal stiffness coefficients, as the
function of |
|
|
|
|
|
Actually, a few examples presented here cannot cover
the entire spectrum of the applications. However they also demonstrate quite
visually, how complex and important solutions can the practice obtain with
the help of the advantages the new non-matrix method to obtain exact
analytical solutions gives. |
|
|
|
|
|
|
|
|
Applications
to the mechanics, acoustics and geophysics |
|
|
|
Applications to the mismatched ladder filters, transmission lines and networks |