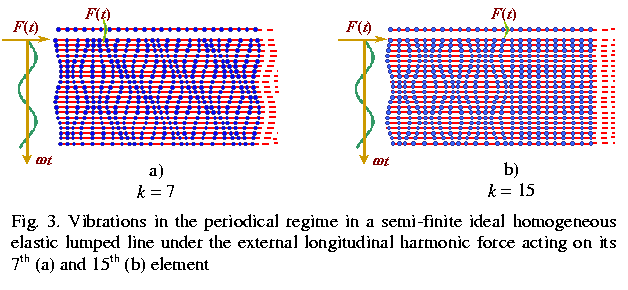
More and more features appear with the models complication. Already when the external force acted on the interior elements of a line, the solutions bifurcate. In a semi-finite line between the external force application point and the line end there arise standing waves, while at the semi-finite end the progressive waves remain (see Fig. 3a). At the conditions determined by the line parameters and vibration frequency, the amplitude in the infinite part vanishes (see Fig. 3b). But any attempt to find these conditions conventionally, by way of superposition of an incident wave and the wave reflected from the bound, will not lead us to an exact result. First, the phase delay of the kth element depends in a complex way on the frequency and line parameters, and second, the vibration amplitude at the free end will not be maximal. |
|
In case of an external force acting on an interior element of a finite line, this last also bifurcates into two sections whose amplitudes are determined by their lenghts and vanish at definite conditions, while the vibrations in the second part generally remain. This problem was solved for some types of lines by Krylov with the help of indirect techniques [6]. |
|
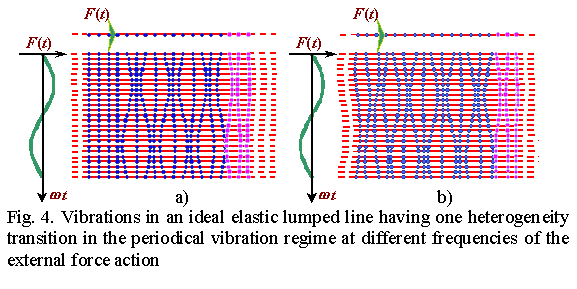
A few vibration regimes can exist simultaneously when transiting to heterogeneous elastic lines. In Fig. 4 the vibration diagrams are shown for the line having one heterogeneity transition in case when its light part (left in each diagram) vibrates in the periodical regime, and heavy part (right in each diagram) vibrates in the aperiodical regime. The same as in the previous model, in Fig. 3, between the external force action point and the heterogeneity transition the standing waves set up, and in the semi-finite section of the light part the progressive waves propagate. With it, in the hard part the antiphase damping vibrations take place. Comparing Figures 3 and 4, we see that the same effects are present in these models. This proves that the aperiodical regime describes the pattern at finite characteristics of an elastic line, i.e., when we cannot present the model as an absolutely rigid system or having an infinite pliability. The solutions corroborate it, transforming into those for related models when the mass of one part of line turning into zero or infinity. |
|
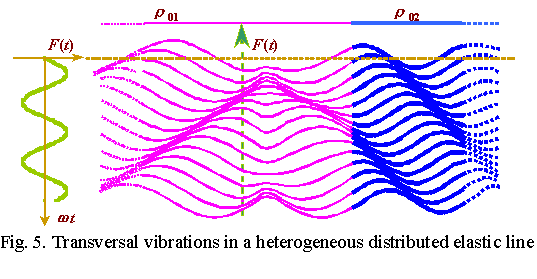
Some features of this process retain at the limit passing. In Fig. 5 we present the vibration pattern in a distributed line having one heterogeneity transition; we have obtained them by way of the limit passing of the solutions for a lumped line. One can see that between the external force action point and this transition the complex-form standing waves form. And again, one cannot obtain this vibration pattern by the superposition, though the delay phases considered above vanish in this case. With the partial reflection from the bounds it is practically impossible to take into account exactly all amplitude and phase characteristics by jointing the solutions of the wave equation for both parts of an elastic line. But when using the limit passing, the matching occurs automatically. And changing the model parameters, one can investigate the elastic system behaviour at the entire range.
|