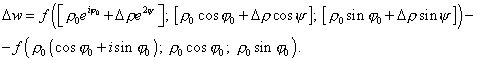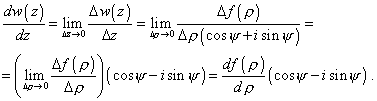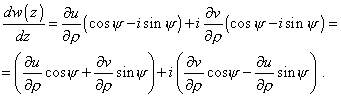SELF

86 - 88

S.B. Karavashkin and O.N. Karavashkina

This derivation shows also the independence of the total differential of the way, how z is represented.

And at = 0

If we now distract from the way how we compared the partial differentials dx, dy and superimpose the limits taken from the system (11) with (20), we yield

i.e. the known value of total differential. This fully corroborates that we were right when identified dz as (20) with the total differential.

Now let us determine the differential of w at the point w₀ under condition that there

87

exists the one-valued map of the -vicinity of the complex plane z into the -vicinity of the complex plane w. As we showed above, in the most general form the function of complex variable can be written as

The increment of the function at the point w₀ will be

We see from (21) that w depends, just as z , on one variable . Thus, we may write

and

If we use the yielded values of differentials of independent variable z and complex function w( z ), it will be not difficult to yield the expression for the total derivative of the complex function. For it, we can make use of (9), (20) and (22):

To find the form, how can we express the total derivative of complex variable of z presented in coordinate form, let us use (2). Then (23) will take the following appearance: