СЕЛФ |
Новогодний вопрос Лео |
| С.Б. Каравашкин | |
|
|
СЕЛФ |
Новогодний вопрос Лео |
| С.Б. Каравашкин | |
|
|
Письмо Лео ко мне От: xu xu <xuszxu@yahoo.com>Кому: Сергей Каравашкин selflab@go.com, selflab@mail.ru Дата: Thu, 18 Dec 2003 09:56:31 -0800 (PST) Тема: проблема с формулой дивергенции
Уважаемый Сергей, У меня вопрос по твоей формуле дивергенции. Посмотри пожалуйста прикрепленный файл. С Рождеством! Лео Приложение: problem.pdf |
|
| В сферических координатах электрическое поле в точке Р, создаваемое диполем Il , имеет вид [1]: |
|
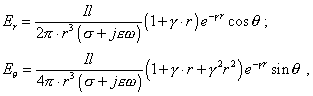 |
|
| где |
|
| Естественно, что направление
распространения электрического поля |
|
| (1) | |
| мы имеем | |
| Однако легко убедиться, что | |
| Я думаю, что проблема в том, что
(1) неверно. Ссылка [2] не вносит вклада стороны
поверхности в дивергенцию вектора, как описано в
(1).
Литература [1] James R. Wait. "Introduction to antennas & propagation", Peter Peregrious Ltd, London, Unided Kindom, 1986, pp 89. Equation (5.30) - (5.31)[2] S.B. Karavashkin "Transformation of divergence theorem in dynamic fields" |
|
| Мой ответ Лео Дата: 22.12.03Уважаемый Лео, Ваше представление о
сферическом диполе, которое Вы почерпнули из
Джеймса Вейта, безусловно, похвально. Но я был бы
Вам ещё более признателен, если бы Вы прежде, чем
сравнивать приведенные Вами выражения для
дивергенции потока от сферического диполя с
выражением для дивергенции вектора в
динамических полях из моей работы,
проанализировали бы вывод самих уравнений из
Джеймса Вейта. При этом Вы нашли бы много
интересного - того, что не видно из конечных
формул. Проверьте внимательно, причём не чисто
механически, а феноменологически, анализируя,
что откуда берётся и почему. Тогда поймёте
причину. У меня, к сожалению, нет книги именно
Джеймса Вейта, но я могу Вам помочь в анализе,
основываясь на решении аналогичной задачи у
Кугушева [1]. В этой задаче также исследуется
электрическое и магнитное поле провода с током
при длине провода l << |
|
|
(1) |
| где Чтобы понять причину, обратим
сначала наше внимание на тот факт, что решение (1),
как и Ваши решения, получено путём подстановки
значения векторного потенциала |
|
|
(2) |
т.е. окольным путём. Сначала
находим вектор |
|
|
(3) |
Таким образом, мы дважды пропускаем выражение (1) через фильтр, отсекающий продольную компоненту. Факт, что в результирующем выражении эта компонента сохраняется, обусловлен тем, что, вдобавок ко всему, мы теряем очень важное слагаемое в выражении для электрического поля. Действительно, если согласно [2, с. 41], до модельных расчётов мы подставим первое выражение из (2) в закон Фарадея, то при этом получим: |
|
|
(4) |
| или | |
|
(5) |
"Последнее уравнение показывает, что вектор |
|
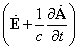 |
|
остаётся потенциальным вектором, т.е. может быть представлен в виде |
|
|
(6) |
| где |
|
|
(7) |
| При этом второе
слагаемое, связывающее электрическое поле с
магнитным, выражает закон электромагнитной
индукции Фарадея" [2, с. 42].
Таким образом, мы пришли к известному выражению, связывающему напрямую скалярный и векторный потенциалы с электрическим полем в пространстве, с уверенностью, что в промежуточных операциях никакая компонента поля не была изъята. Чтобы на этой основе определить правильную зависимость электрического поля от времени и координат, мы должны сделать ещё одно отступление от изложения и обратить внимание на саму запись векторного потенциала. Согласно Кугушеву, выражение для векторного потенциала, на основе которого он получил выражение (1) для напряжённости электрического поля, имеет вид [1, с. 98]: |
|
|
(8) |
При этом следует отметить, что данное выражение не является точным решением волнового уравнения для векторного потенциала, что очень важно для дальнейшего изложения. Действительно, как известно, выражение для векторного потенциала находится на основе волнового уравнения типа [1, с. 88] |
|
|
(9) |
где |
|
Но решением этого уравнения является не функция (8), которая нами исследуется, а интегральная функция типа [1. с. 89], [3. с. 95]: |
|
|
(10) |
Однако "для области r >> l можно считать все точки диполя равноотстоящими от исследуемой точки поля, вследствие чего (10) можно переписать в виде |
|
|
(11) |
где e3 орт, параллельный направлению тока. Так как jm = Im/S и Sl = V , S - сечение проводника, получаем |
|
|
(12) |
Переходя к сферической системе координат, в которой |
|
|
(13) |
| получаем формулу (8),
определяющую векторный потенциал на расстоянии r
>> l " [1. с. 97]. Таким образом, (8)
определяет векторный потенциал только для
дальней зоны, когда согласно [5], все параметры
волнового процесса стабилизировались. Поэтому,
когда исследователи (в том числе и сам Кугушев)
применяют для ближней зоны результаты,
полученные на основе данного векторного
потенциала, то это они делают неправомерно,
поскольку этим они нарушают условия задачи.
Отсюда возникает сомнение в правильности
выражения (1). Если выражение (1) описывает процесс
в дальней зоне, то никаких суперпозиций
напряжённости поля с разными характеристиками
затухания и разными сдвигами фаз в выражении
присутствовать не должно. Это дополнительно
подтверждает высказанное выше утверждение о том,
что вывод выражения (1) был произведен
некорректно.
Чтобы получить правильное
выражение для напряжённости электрического поля
на основе выражения (7), нам нужно определить
скалярный потенциал |
|
|
(14) |
Учитывая, что в нашей задаче |
|
|
(15) |
мы можем записать |
|
|
(16) |
или с учётом (8) |
|
|
(17) |
При этом слагаемые в правой части (7) для напряжённости электрического поля можно записать в следующем виде: |
|
|
(18) |
|
(19) |
Таким образом, |
|
|
(20) |
| Как мы видим из данного
выражения, продольная и поперечная компоненты
поля имеют вполне стабилизировавшееся затухание
в пространстве при степенях затухания, вполне
соответствующих рассматриваемой модели. При
этом фаза поперечной составляющей сдвинута по
отношению к продольной на 90о, что ещё раз
подтверждает справедливость утверждения о том,
что калибровка напряжённости электрического
поля некорректна, поскольку потенциальная
составляющая поля имеет свои характеристики
процесса распространения в пространстве,
отличные от поперечной компоненты.
Теперь, на основе скорректированного, а главное, полного выражения для напряжённости электрического поля, сравним дивергенцию напряжённости этого поля с результатами доказанной мною теоремы о дивергенции вектора в динамических полях [6] (странно только, что, хорошо оформив свою заметку, Вы не заметили, что эта статья опубликована в международном журнале Archivum mathematicum, 37 (2001), 3, с.233-243. Ссылку без издания неприлично представлять, как Вы думаете? ;-)). Для проверки воспользуемся стандартной формулой, приведенной в Вашей заметке: |
|
|
(21) |
С учётом (20), первый член правой части будет иметь вид |
|
|
(22) |
Соответственно второй член примет вид |
|
|
(23) |
В результате имеем |
|
|
(24) |
| Как мы видим из (24), дивергенция
электрического поля не равна нулю и фаза её
изменения во времени смещена на 90о по
отношению к фазе продольной составляющей, что
вполне соответствует феноменологии
распространения волнового процесса в
пространстве.
Несложно проверить, что и амплитудное значение дивергенции вектора напряжённости электрического поля в Вашей задаче тоже соответствует доказанной мною теореме о дивергенции вектора в динамических полях. Для этого воспользуемся выражением (1) Вашей заметки, которое Вы вполне правильно интерпретировали, и продолжим его до результата: |
|
|
(25) |
| Так что можете
с превеликим удовольствием сравнивать (24) и (25).
Как видите, в действительности проблем с
теоремой нет. Есть проблемы только с
существующими решениями для конкретных моделей.
Я уверен, что, если Вы аналогично проверите вывод приведенных Вами выражений у Вейта, то получите аналогичный результат, который удовлетворяет доказанной мною теореме. Правда, в дополнение к данному выводу Вы должны внимательно проанализировать дополнения, вносимые в выражение для векторного потенциала вследствие конечной проводимости пространства. Если же вернуться к разговору о справедливости теоремы, доказанной мною, то её можно опровергнуть только, найдя ошибку в самом доказательстве, поскольку теорема первична по отношению ко всем решениям моделирующих уравнений. И это не моё желание. Это объективность построения любой теории. Сначала формулируются базовые теоремы (в данном случае - теоремы сохранения для динамических полей), потом строится математический аппарат, а потом решаются задачи по моделированию конкретных процессов. Так строил свою систему Максвелл, так нужно и дальше развивать теорию ЭМ полей. Хочу особо отметить, осознанно или нет, но Вы подняли очень интересный и важный вопрос, который требует и своего осмысления, и своего решения. Если у Вас есть серьёзное желание нырнуть в глубь данного вопроса, я с удовольствием готов Вам помочь. С новым годом Вас и с новым знанием. Сергей.
Литература: 1. Кугушев А.М., Голубева Н.С. Основы радиоэлектроники. Линейные электромагнитные процессы. Москва, Энергия, 1969, 880 с.2. Левич В.Г. Курс теоретической физики, т.1. М., Государственное издательство физико-математической литературы, 1962, 695 с. 3. Ландау Л.Д., Лифшиц Е.М. Теория поля. - // Теоретическая физика, т. 2. М., Наука, 1973, 504 с. 4. Каравашкин С.Б. К вопросу о продольных электромагнитных волнах. Глава 1. Снятие запретов. SELF Transactions, 1 (1994), 15-47, http://angelfire.lycos.com/la3/selftrans/archive/archive.html#long 5. Каравашкин С.Б., Каравашкина О.Н. Сравнение характеристик ЭМ и акустического полей. SELF Transactions, 2 (2002), http://angelfire.lycos.com/la3/selftrans/v3_1/contents3.html#taew 6. Каравашкин С.Б. Трансформация теоремы о дивергенции в динамических полях. Archivum mathematicum, 37 (2001), 3, 233-243. SELF Transactions, archive, http://angelfire.lycos.com/la3/selftrans/archive/archive.html#div
|
|