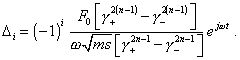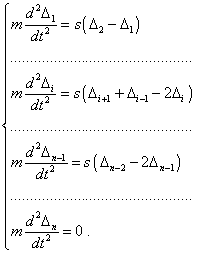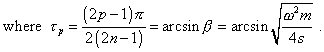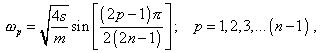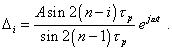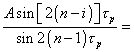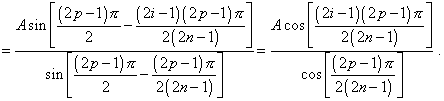Volume 4 (1999), No 4, pp. 5-13

11

Solutions for finite elastic lumped lines

For the aperiodical regime at >1

Finally, for that critical at =1 the solution has the following form:

The force is absent in the first equation; this makes a difference from (41) for the system of equations describing free vibrations in the studied line. It has the following form:

The given vibrations arise in an elastic system when

Proceeding from (46), the natural frequencies are determined by the expression

and the equation of vibration has the form

Comparing with the line with unfixed end, we really see considerable changes in the presented solutions, though the block structure in the form of ratio of trigonometric functions remained.

For the forced vibrations, the changes relate to the resonance frequency, because the conditions of its rise took the form

The same for the conditions determining the amplitude minimum:

It follows from the conditions (49) and (50) that when we fixed one of the line ends, in the amplitude regularity in the maximums and minimums shifted, and not by a quarter of a period, as one could expect, but some more, because in the left parts of these expressions we see the value (2n - 1 ) , not 2n, as it was in (14) and (15). This difference disappears when the number of line elements growing and when the gradual transition to the distributed line. When reverse transition, this difference is non-restored.

For free vibrations, the amplitude dependence on the mode number is determined by the conditions which we can set up after the following transformation of the amplitude part of solution (48), noting (46):

The yielded expression (51) shows that as the number of mode p grows the denominator of the expression decreases similarly to (33). It means, the amplitude of free vibrations, the same as in a free-end line, grows monotonously with the growing mode number and reaches the maximum at p_max, but for a lumped line it never reaches an infinite value.

To complete this analysis, make certain that the presented expressions are the solutions. It is simple to do so by their direct substitution to any related equation of the modelling systems, by analogy with the above models. For example, substitute (48) to the last but one equation of (45). We yield: