Materials.Technologies.Tools |
22 |
S.B. Karavashkin |
|
|
|
Materials.Technologies.Tools |
22 |
S.B. Karavashkin |
|
|
|
At the same time we should mark, the periodical regime of free vibrations in a semi-finite line corresponds to that in finite lines for which the vibrations having a form of standing waves are typical. This is caused by the fact that the yielded solutions describe stationary processes where every line element has some finite vibration energy being non-time-scattering and non-transmitted to other elements due to an ideal pattern of a line, because the neighbouring elements have similar energy. It means, in this aspect the difference between finite and infinite lines disappears, although the total vibration energy for finite and infinite lines will be different. 3.2. Infinite line The homogeneous differential system for the considered model is |
 |
(49) |
As in previous cases, in an infinite line free vibrations can exist in three usual regimes with usual conditions of their origin. In the periodical regime at |
| (50) |
free vibrations have a form of stationary travelling wave able to propagate both with the growth of elements number (with the negative sign before the delay phase) and with the number decrease (with the positive sign). With it the vibration amplitude in the whole allowed frequency range is constant and determined by the initial conditions of a problem. In general case in periodic regime there can arise also a standing wave, if after the initial conditions – or rather after the preceding action parameters – the solution has a form of superposition of two above-described oppositely-directed waves. To a definite extent it unites the solutions for periodical regime in an infinite line and the same in a semi-finite one. In the aperiodical regime at |
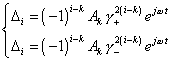 |
(51) |
two oppositely directed damping processes are possible,
too. Basing on the above interpretation, they correspond to the energy applied to the
system at plus- either minus-infinite point of the line, because In critical regime at |
| (52) |
we can see the anti-phase vibrations of elements with the amplitude constant along the line. Besides, we should point out that the forced vibrations in an infinite line have not critical regime. We should mark also that the same as in the beginning of this item, all presented solutions satisfy the homogeneous system of equations. 4. Completeness and bounds of solutions applicability In the items 2 and 3 we have presented the analysis of solutions describing forced and free vibrations relatively. We yielded these solutions for stationary vibrations, which was determined in case of forced vibrations – by the pattern of external force affecting the line, and in case of free vibrations – by the harmonic pattern of vibration of the kth element. As is known and as was pointed before, when the external force affecting starts or finishes, the transients arise in the line. They can be modelled on the principle of superposition of vibrations constituting the spectrum of transit function. With this extent, the yielded solutions can describe the versatile models of complex transients. Just due to the solutions being exact and analytical, there arises, for example, the scope to study the wave front transformation in its along-the-line propagation, when the pulse of most complex spectral composition was assigned, and other problems. On one hand, in accordance with [4, p. 115], completeness of yielded solutions is determined by the fact that in their assemblage they satisfy both homogeneous and heterogeneous differential systems. On the other hand, the solutions cover the whole range of frequencies from zero to infinity. And unlike the known solutions (2), our complete solutions have quite complex and diverse form varying dependently on the parameters of both affecting force and the system of material bodies itself. |