V. 1 |
57 - 61 |
| On the new class of functions | |
|
|
V. 1 |
57 - 61 |
| On the new class of functions | |
|
|
57 On the new class of functions being the solution of the wave equation S. B. KaravashkinSpecial Laboratory for Fundamental Elaboration SELF e-mail: selftrans@yandex.ru , selflab@mail.ru We will prove that not only the commonly known explicit time-delay functions but implicit functions also are the solutions of second-order wave equation. This class of implicit functions is the covering solution of the wave equation. This considerably broadens the area of wave equation application onto the modelling of wave processes in nonlinear media Keywords: mathematical physics, wave physics, wave equation, implicit functions, modelling of nonlinear wave equations Classification by MSC 2000: 35G20, 35J05, 35L05, 35L10 Classification by PASC 2001: 03.65.Ge, 41.20.Cv As is known, the differential hyperbolic equation |
| (1) |
has the general solution (see e.g. [1, p. 300]) |
| (2) |
where c = Up to now this solution was thought to be unique, as it was stipulated for the theorem of unique solution of differential equation. None the less, there exists one more class of functions being the solution of differential equation (1) but not taken into account by the solution (2). General form of this class of functions is |
| (3) |
where 58 In other words, this solution belongs to the class of implicit functions whose behaviour and techniques to differentiate and integrate them much differ from those for explicit functions. While for explicit functions we have a definite systematisation of differential equations, and for a definite class of these equations we have the regularities and schemes to find the solutions, for implicit functions this tool yet is not available. So it is quite natural that now the solution (3) can be checked for (1) only by a simplest method of direct substitution. To do this substitution, let us find the first and second partial differentials of x and t of (3), basing on well-known laws of differentiation of implicit functions. To simplify the computations, consider a half of right part of (3): |
| (4) |
where A = kx - |
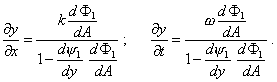 |
(5) |
59 The second derivatives after we transform them and substitute (5) will take the form |
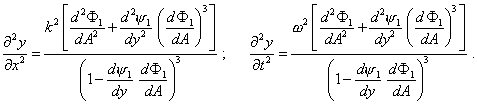 |
(6) |
Substituting (6) into (1), we yield the required. The same we can prove the correspondence of the second part of (3) to (1). Thus, (3) determines the whole class of implicit functions that satisfy the linear wave equation. The presence of a new class of functions being the solutions for (1) not a least violates the theorem of unique solution of differential equation, as at |
| (7) |
(3) degenerates into (2). Thus, we have proven that the solution known before was a particular case of more general class of functions. Outwardly it can seem that the adduced computations do not contain any valuable information and the yielded class of functions (3) can be described by (2). 60 But let us consider this point more profoundly. The found
class of implicit solutions defines a nonlinear wave whose degree of deformation depends
on the behaviour of functions |
the solution of the wave equation (1) describes a
progressive wave propagating along the axis x being inclined by some angle |
|
illustrate the direct dependence of the degree of curve
deformation on |
i.e. the dependence on the amplitude being proportional to
the energy of vibration, we will yield the direct continuous passing from the quasi-linear
vibrations 61 |
Fig. 1.
|
The second important fact related to the class of implicit functions is the fully changing understanding of the physics of running processes, especially in the area between the linear and nonlinear modes of processes. As is known, in the continuum theory all wave processes are strongly subdivided into two classes - linear and nonlinear processes. “In cases when the assumption of smallness of the sought functions was admissible, in the statement of problem we can make a linearisation that is reduced to the following considerable simplifications: |