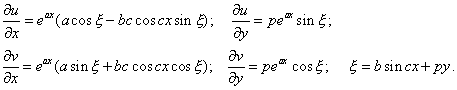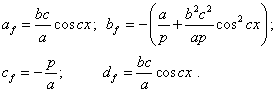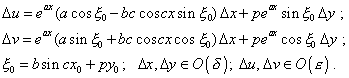102

S.B. Karavashkin and O.N. Karavashkina

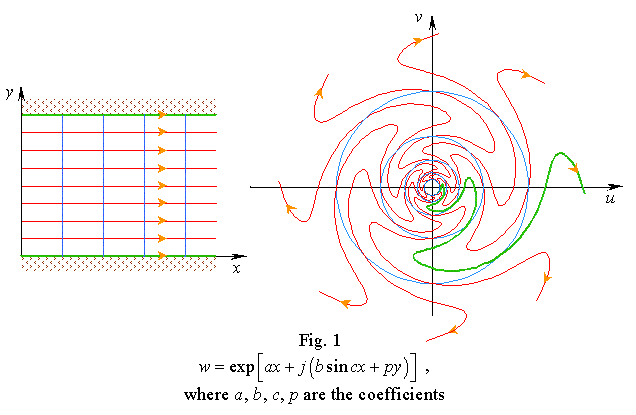
We can prove easy that the conditions defining the classes of functions that implement the conformal and quasi-conformal mapping are incomplete to define the general set of analytical functions. In such way we show in Fig. 1 the mapping implemented by the function

where a, b, c, p are some constants. As we see from the construction, this function implements the one-valued continuous mapping of a semi-finite belt of a plane Z  onto outside of the circumference of the plane W (the negative semi-finite belt will map inside this circumference, and in this domain the mapping will be also one-valued and continuous). Of course, (4) does not satisfy the Caushy - Riemann conditions. Apply the above conditions of "quasi-conformity" (2) and (3) to (4). The first particular derivatives of w  with respect to  x and  y  will have the following form:

Substituting (5) into (2), we can determine the coefficients that still were unknown:

And substituting (6) into (3), we yield

We see from (7) that the condition (3) is not true for (4). With definite values of parameters and coefficients included in A, its value can be negative or sign-alternative. At the same time the construction in Fig. 1 displays that the mapping is one-valued and continuous; hence, it satisfies the analyticity conditions. Along with the fact that (4) does not satisfy (3), we can easy show that (4) maps the infinitesimal circumferences of the plane Z into the infinitesimal ellipses of  W, which is typical just for quasi-conformal mappings. Actually, for any  - vicinity of the point z₀ = x₀ + jy₀  in the domain of the plane Z being mapped into the -vicinity of the point w₀ = u₀ + jv₀  of the plane W, we can write for (4) as follows:

For any fixed point of the domain the system (8) is equivalent to the system

where A₁, B₁, C₁, D₁  are the constants varying only with the changing co-ordinates of the selected point on the plane Z. But (9) maps (in case of the studied function) a circumference into ellipse, because, in accord with (8), all above coefficients in the domain Z are limited functions; therefore one always can find such small (x,y) that will satisfy the condition w() . This just proves the stated.