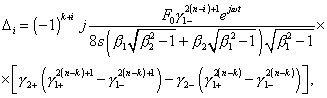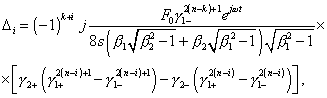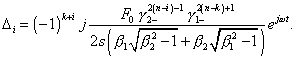V.2 No 1

65

On solution for an infinite heteroheneous line

In the second section of elastic line, the pattern of aperiodical process will be much more complex because of influence of the square brackets expression in the right part of solution (18). The presence of phase shifts ₂ will depart from the rigorous antiphase pattern of neighbouring elements of section and the regularity of damping degree by the frequency will be complicated.

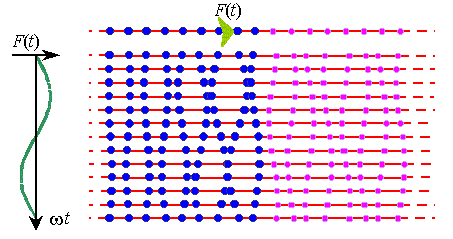
Fig. 3. The vibration diagram in a heterogeneous elastic line at 22,7 Hz. The external force affects the heavier part of line; the frequency is between the boundary frequencies for the light and heavy parts of line;   F₀ = 0,6 N ; s = 100 N / m ; m₁ = 0,01 kg ; ₀₁ = 200 s ^{- 1} ; m₂ = 0,02 kg ; ₀₂ = 141,42  s ^{- 1}

In the third section the progressive wave propagates. Its amplitude is proportional to , i.e. to the damping degree in the heavy part of line. As we see in Fig. 3, the vibration amplitude in this section can be well less than the vibration amplitude in the region of external force application, despite when plotting, we chose m₁ = m₂, so the external force application point was closed to the utmost to the heterogeneity transition. It evidences the residual pattern of vibration process in the third section of line.

As the next typical transformation of basic solutions, consider the case when condition (8) is true for the whole line.

3.4.

In this case we have to apply the transformation (9) both to the light and heavy parts of line. The result will be following:

for i k

for k i n

and for i n + 1

We see from (21)–(23) that in all three sections of elastic line the aperiodical regime settles. None the less, in each section it has its distinctions. In the first section the degree of along-line damping is determined by the multiplier , in the second section – by the square bracket expression in the right part of solution (22), and in the third section – by the multiplier . In each case this influence reflects not only on the base of power but also on its index and even on the type of function.

The common salient feature of solutions (21)–(23) in comparison with, e.g., [1] and [2] is the phase shift by (-/2)  in the first and second sections; the imaginary unity in the right-hand parts of (21) and (22) determines it.

Thus, having studied the transformation of solutions (2)–(4) dependently on, whether it completely or partially satisfies the condition (8), we see that account of the aperiodical regime in case of elastic infinite line allows us studying much more completely all the variety of vibration pattern possible in a line. It helps to analyse better the possible transformations of vibration pattern dependently on the parameters of elastic system and external force, as well as to reveal more completely the most dangerous and stressed sections.