SELF |
44 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
44 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
Actually,
for this circuit the impedances |
| (31) |
In
accord with (9) – (11) and (31), the parameter |
| (32) |
where |
With it
the parameter |
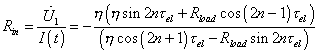 |
(33) |
where |
The
typical form of the amplitude (a) and phase (b) of the input impedance with respect to
frequency
|
|
Fig. 6. The calculated amplitude-frequency (a) and phase-frequency (b) characteristics of the input resistance Rin at different active load values Rload and constant input current value I (t) with respect to frequency. The investigated filter parameters: L = 12,6 mH; C = 0,5 mF; R0 = 159,15 Ohm; rL = 10 Ohm; R1 = 20 kOhm; R2 = 33 kOhm; Rload = 0, 51, 102, 158, 358, 558, 758, 958 Ohm. |
Contents: / 35
/ 36 / 37 / 38 / 39 / 40 / 41 / 42 / 43 / 44 / 45 / 46 / 47 /