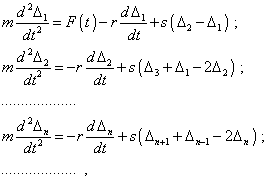СЕЛФ

18

С.Б. Каравашкин и О.Н. Каравашкина

В качестве второго фактора следует отметить существенную неполноту решений, которые могут быть получены существующими методами. Как показано в [10]- [13], существующие методы не позволяют исследовать колебания в закритической области (выше граничной частоты 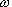₀). “Решение краевых задач теории колебаний сводится, по существу, к определению собственных значений, связанных с собственными частотами или другими параметрами исследуемой системы и нахождению собственных функций (форм колебаний). Если собственные значения и собственные функции найдены, тогда можно считать краевую задачу решенной. В настоящее время разработано большое число приближенных методов нахождения собственных значений, но все они довольно трудоемки, позволяют находить только первые собственные значения и, главное, не объединяют изучение систем с дискретным и непрерывным распределением масс” [5, с. 3- 4]. Только в отдельных частных случаях имеются неполные, ограниченные по применению решения или упоминания о возможности процессов в закритической области (см., например, [7, с. 282- 285], [8, с. 294], [14, с. 109]). В то же время, колебательный процесс в этой области характерен именно тем, что при частотах выше граничной даже идеальная упругая линия ведет себя как естественный демпфер с затуханием амплитуды колебаний вдоль линии. Как будет показано в данной работе, сопротивление оказывает существенное влияние на характеристики данного демпфирования, как и на характер колебаний элементов системы. Учёт этого фактора важен с точки зрения полноты и качества анализа влияния сопротивления на колебания упругой системы. В ходе исследования мы намеренно ограничимся простой моделью одномерной полубесконечной упругой линии, чтобы обеспечить наглядность анализируемых процессов. При этом будем предполагать, что для других типов упругих линий данные выводы могут быть получены аналогично при наличии точных аналитических решений типа приведенных в [10]- [13].

2. Точные аналитические решения для одномерной полубесконечной упругой линии с сосредоточенными параметрами при наличии сопротивления

В поисках точного аналитического решения для исследуемой упругой линии мы не будем идти стандартным путем нахождения частных решений для моделирующей системы дифференциальных уравнений, а попытаемся свести задачу к уже имеющимся в [10] решениям для идеальной линии, тем более что это несложно сделать.

Действительно, моделирующая система дифференциальных уравнений в нашем случае будет иметь вид

- внешняя сила и её амплитуда; m - масса элементов упругой линии; r - механическое сопротивление связей. Здесь и далее n = 1, 2, 3, ..., а s - коэффициент жесткости линии.