SELF |
54 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
54 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
3.2. Transverse Doppler effect Above we saw, if we calculated the change of frequency of received signal by the observer moving non-centrally as to the signal source, the classical formalism will also reveal the transverse effect, but in distinct from relativistic formalism, this effect has a negative sign and essentially depends on the aimed distance.It is easy to yield the relation in frequencies of source and receiver from (9) at the condition |
| (27) |
In this case (9) takes the form |
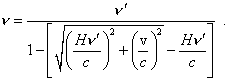 |
(28) |
As we see, in case of transverse Doppler effect, the square bracket in (28) is strongly positive, due to which the value of source frequency will always be more than frequency received by moving observer, and this regularity will essentially change with respect to the aimed distance. In Fig. 8 we see the plots of this regularity at different frequencies of source signal.
|
|
Fig. 8. The change of relation of frequency |
| This regularity shows that from the view of classical
formalism, the transverse Doppler effect rapidly decreases with the distance, but not from
zero value of effect ( The cause of this unexpectedness becomes clear if we look
at the general formula (9) and recall that when finding the longitudinal effect with the
aimed distance lessened to zero, we accounted the change of quadratic bracket of
denominator in transition through the point of signal radiation. Just due to this, there
appeared a sign-alternating term in the expression for longitudinal Doppler effect (15). But to find the transverse
effect, we at once in general case indicated the value of angle |
Contents: / 46 / 47 / 48 / 49 / 50 / 51 / 52 / 53 / 54 / 55 / 56 /