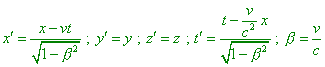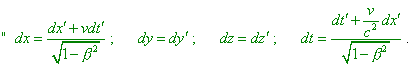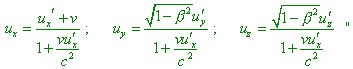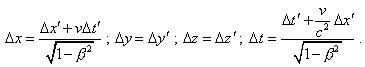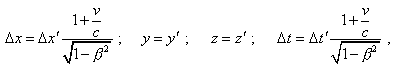V.5 No 2

23

On light aberration

At the same time, thinking the relativistic conception to be self-consistent, we could expect that calculating through the theorem of velocities summing, we would have to yield the same result. This is not so, and we can easily make it sure.

We know that the statement of problem in the theorem of velocities summing is the following: “let in K' be given some motion:

In accordance with (Lorentz transformation - the Authors)

such motion

corresponds to it in K . It is required to establish the relation in components of speed in K':

and related values in K:

[9, p. 31]. Through Lorentz transform inverse to (43), Pauli, after whom we recall the derivation of speed summing theorem, yields

Hence, dividing by the last equation, we found:

[9, p. 31].

Yielded expressions (50) are the commonly known equations that determine the speed summing in relativistic mechanics. From the derivation we first of all see, in distinct from Einsteinian formula (36), the time increment takes its part in transformation of infinitesimal sections (49). It would seem, if the transformation of finite sections of the metric (36) comes to the result discrepant from the view of Relativity, while the theorem of speeds summing gives the ‘proper’ result, the first variant is erroneous and we have to use the second, i.e. the theorem of speed summing, and not in the part of problems but in all studies. Though from another side, it is strange of course, why the observer in the dotted frame cannot compare independently his measure of length with the stationary observer, then to compare the rate of clock, then to measure the speed of light, allowing the stationary observer to count the result on the basis of compared transformations.

Relativists used to conclude unambiguously: “At the first glance this question seems to be hopelessly confused. There exist the opponents of relativity principle, simple minds (?! - Authors) who, having got to know this complicacy in determining the ruler length, with a noble indignation (! - Authors) exclaim: ‘Of course, one can derive whatever, if one uses wrong clock (? - Authors). This is an example, to which extent of absurdity can lead us a blind belief in the magic power of mathematical formulas’, - and crush the theory of relativity in one blow. Our Reader, hopefully, has already guessed, that formulas are not a least the main circumstance, as we deal with the relationships of mere principle, which one can successfully grasp without certain applying to mathematics” [2, p. 240].

Born is right, of course: the discrepancy is in the very phenomenology of Relativity. Mathematical formulas only reflect the presence of discrepancies. But when he says that the opponents of Einsteinian Relativity are against the principle of relativity on the whole, not against the relativistic interpretation of this principle, and that the opponents of Relativity see ‘mistakes’ exceptionally in the wrong clock, - this is an usual trick of relativists, - we see the substitution of the issue by convenient interpretaions. To show it, let us follow Born, how he phenomenologically removes the time parameter from Lorentz transform.

In the relativistic view given by Born, the statement of problem of sections measurement sounds as follows: “Let the ruler of an unit length be located in the origin of reference frame S along the axis x. Let us set ourselves to the question, which is its length in the frame S '. It is immediately clear, this length will differ from the unit length. The observers who move with S 'will, of course, measure the locations of ruler ends simultaneously in the frame S '. But this does not mean ‘simultaneously’ in the frame S. Thus, even if the location of one end of ruler was determined simultaneously by the observers of frames S and S ', the S- and S '-observers will be unable to make the reading of its another end, being simultaneous after S-clock. At the moment when they do it, the S '-frame has been already shifted ahead and the result yielded by the observer in the frame S ' reflects the shifted location of the second end of ruler” [2, p. 240].

It unambiguously follows from this point that the record of intervals in the speeds summing theorem is true; then in the integral form for finite sections we would have to use not Einsteinian formula (36) but the expression that follows from (49),

But what follows from this formula with the above statement of problem? If in the stationary reference frame S, t means time necessary the light beam to pass the section x, and accordingly, in the frame S '  the time interval  t'  means the time necessary the beam to pass the section x', we have the right, on the basis of Einstein’s postulate of light speed constancy in all reference frames, to eliminate the time from (51):

or

We yielded the transformation (53) basically different from (36). In particular, in change of velocity direction of the frame S ', the under-root expressions in the right parts change their sign, while (36) does nor depend on direction of the frame motion, - and this is the matter of principle.

It also follows from (53) that if we some refine the technique to measure the lengths, retaining all features pointed by relativists, we will be able to transmit a non-distorted spatial and time metric between the mutually moving frames, in full contradiction to the relativistic statements that this operation is impossible. Actually, if we, noting (53), add to Born’s technique that the measurement has to be made twice: once in motion of S ' in positive direction and second time - in negative direction, we will yield in the first case

where x'_A and t'_A  are measured in S '  length of ruler which is located in the stationary frame, and the time necessary, the beam to pass the distance between the ends of this ruler from the view of moving reference frame.

In the second case, when S '  moved in the negative direction, we yield

Multiplying the left and right parts of (54) and (55), yield