SELF |
32 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
32 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
3. The law of vectors summation with Lorentz transformation In this item we will check the validity of the law of
vectors summation in IRFs which is known to be the basic law both in studying of the
trajectories of bodies motion and for finding the first and following derivatives. In
general case, when differentiating, we always seek the difference in vectors - it means
that the validity of vectors summation law in fact defines the legacy of differentiating
and integrating in space in which we perform this operation. It is also known and long ago
proven that in classical formalism, in limits of IRFs, this law is absolutely true. “Equations of mechanics have an identical form in any inertial
reference frames” [10, p. 73]. With it, “the
constancy (invariance) of laws of mechanics in Galilean transformations is the content of
the relativity principle of the Newtonian mechanics” [ibidem]. It is easy to
show it again. Let we have two Galilean reference frames K and K'
mutually moving along the common axis x with the speed v, and
let with respect to the frame K there moves some material point with velocity
If both calculations come to the same result, the law in this mathematical formalism is true. If the results are different, the law in this formalism is violated. Such check is common, as it does not require the equal modules either retained inclination angles of vectors in transformation, but only clears, whether the formalism is closed. This has to provide the result of calculation independently of the way in which we calculated. This principle of closed formalism undoubtedly has to remain true in IRFs, where the space is not warped. In classical formalism it is checked very simple. In direct transformation of the vector of speed |
| (39) |
whence |
| (40) |
On the other hand, transforming the x-projection of speed, we have |
| (41) |
and accordingly for the y-projection |
| (42) |
From this, (41) and (42) fully coincide with (40), which corroborates the law of vectors summation true in Galilean RFs. In relativistic mechanics, with all outward simplicity of the check, it is not so obvious. To show it, let us first determine the module of velocity of the point in the RF K' with direct transformation of vector. In this case the point moves in the plane, so in accordance with the law of relativistic speeds summation |
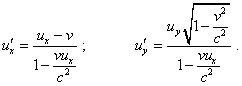 |
(43) |
Thus, |
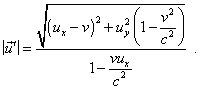 |
(44) |
Now let us try to yield (44) through transformation of
projections of |
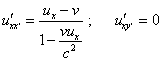 |
(45) |
and for y-projection, accordingly, |
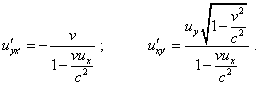 |
(46) |
As in transformation the y-projection gains the projection in x' , |
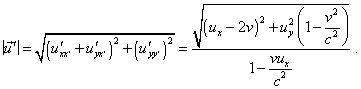 |
(47) |
Comparing (44) and (47), we see different results. This means, in relativistic formalism the law of vectors summation in transformation from one IRF to another is not true. With it, we may not state that only the way of direct transformation of vector is true but the way of transformation of projections of vector is untrue, as we might say, basing on the standard relativistic statements like the following. “But we cannot use one kinematics for one amount of physical phenomena and another - for another amount, requiring the invariance in relation to Galilean transformation for mechanics and invariance in relation to Lorentz transformation for electrodynamics. However, we know that the first transformation is the limiting case of that second, just the case in which the constant c is infinitely large. Accordingly, following Einstein, we will premise that classical mechanics is not strongly true but rather needs to be some modified. The laws of new mechanics have to appear invariant with respect to Lorentz transformation” [11, p. 261]. To estimate the degree of Born’s statement, we have to draw our attention that the very his statement has a stipulation to check, whether Galilean and Lorentz transformations are compatible. If we agree that the invariance of Lorentz transformations generally has not to be identical to Galilean invariance, we at the same time, tending the value of speed of light to infinity, have to yield (44) and (47) coinciding. But we yield in the first case |
| (48) |
and in the second |
| (49) |
Thus, in the limit passing to Galilean RF, we also do not achieve the equal results of transformation; this evidences of untrue law of vector summation in formalism containing Lorentz transformation. Noting this feature, we already may not establish any relations in vectorial projections, may not differentiate, may not consider the law of angular momentum conservation for a system of bodies, as the very angular momentum is a vectorial value and in the course of proof we have to sum the momenta of bodies which the system contains. Also, in relativistic formalism the study of dynamic behaviour of bodies loses any sense, as the result of modelling will depend not on the regularities of phenomena but on the chosen way of calculation. |
Contents: / 29 / 30 / 31 / 32 / 33 / 34 / 35 / 36 / 37 / 38 / 39 /