V.6 No 1 |
11 |
| On excited state of orbital electron | |
|
|
V.6 No 1 |
11 |
| On excited state of orbital electron | |
|
|
In passing from the complex solution to that real, if the initial expression for the exciting force (60) contains only a real part, (77) will transform to the following appearance: |
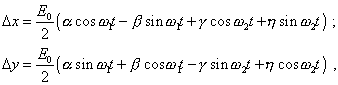 |
(78) |
where |
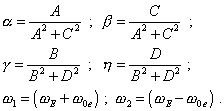 |
Then, taking |
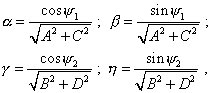 |
(79) |
yield |
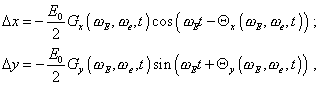 |
(80) |
where |
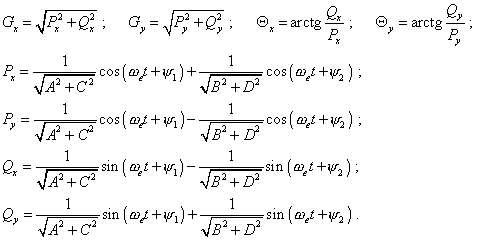 |
The yielded solutions (80) show, the electron’s
excited orbiting is a complicated oscillation dependent on the frequency of oscillations
in a stationary orbit and on the frequency of affecting force. With it, the periodicity of
oscillation that provides the atom’s maximal radiation at the excitation frequency
will take place only at the frequency
|
|
Fig. 10. The scheme to calculate the relation between the inertial reference frame and the frame of electron moving in the stationary orbit
|
But before we, basing on (80), yield the final solution, we have to pass to the inertial reference frame, Fig. 7. It will be easy, given in accordance with Fig. 10 |
| (81) |
With the relation (81), the solution (80) describes excited motion of electron in a weak external electric time-variable field. |
Contents: / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11 / 12 / 13 / 14 / 15 /