SELF |
50 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
50 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
To determine the angles of inclination of the electric field vectors produced by the skeleton and orbital electron, make use of the graph in Fig. 12.
|
|
Fig. 12. The scheme to find the inclination angles to the axis x of the electric field vectors of the atomic skeleton and orbital electron
|
From the |
| (33) |
or with account of (25) and (26) |
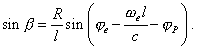 |
(34) |
We also have from the graph in Fig. 12 |
| (35) |
It follows from (35) that |
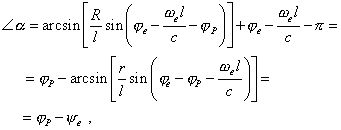 |
(36) |
where |
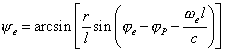 |
Thus, with account of (36) and Fig. 12, we can write the electric field vectors of the orbital electron and skeleton in the complex form as follows: |
| (37) |
where, according to (23) and (32), |
| (38) |
and |
| (39) |
It follows from (39) that the dynamic field of atom in polar coordinates has both radial and tangential projections, as the amplitude part of (39) is complex. This is quite expectable, as the electron’s orbiting unavoidably causes the tangential component of the field. We already may not reduce it to the model of shallow potential well, as the adherents of quantum conception tried. This field will be not only dynamical but also sign-alternating. The dynamic diagram of radial projection is shown in Fig. 13.
|
|
Fig. 13. The dynamic diagram of radial component of the field of atom
|
As we can see from the diagram, at any point out of the electron’s orbit, the repelling (in the diagram – positive values of the z-projection) alternates in time with attraction (negative values of the z-projection) when the electron flies farer from the observation point of field. This alternation is periodic and determined by the frequency of electron’s orbiting. The amplitude of field is localised in the near of atom, at the distance of several radii of the orbit of exterior electron it is insufficient. When analysing this diagram, we have to account, this scheme is quite simplified, as we ignore the field of electrons within the skeleton of the atom. The real field will be, of course, much more complex, but the main feature – the sign-alternating periodic field in the near of atom – will remain, as it is caused by the dynamic pattern of atomic structure. Namely in this field there will occur the scattering of exterior electrons which we will study in the next section. Finishing with the dynamic field of atom, we would like to visualise in Fig. 14 the x-projection of the drawn field with which we will operate in studying the scattering of electrons in the atom.
|
|
Fig. 14. Dynamic diagram of the x-projection of the field of atom. The positive values of the electric field vector related to the positive direction of the x-axis are with the positive direction of the z-axis (to the top)
|
In the diagram we see some transformed, comparing with Fig. 13, appearance of the field which, none the less, remains the above features – sign-alternating periodical field. |
Contents: / 43 / 44 / 45 / 46 / 47 / 48 / 49 / 50 / 51 / 52 /