т.6 No 1 |
17 |
| Методика поиска решения некоторых типов нелинейного волнового уравнения | |
|
|
т.6 No 1 |
17 |
| Методика поиска решения некоторых типов нелинейного волнового уравнения | |
|
|
3. Методика нахождения решения волнового уравнения типа u’’ + g(u)u = 0 Теперь пользуясь методикой, отработанной на первой задаче, найдем решение дифференциального волнового уравнения для случая, когда коэффициент g зависит от u, т.е. |
| (31) |
При этом в данном выражении мы намеренно не представляли второе слагаемое левой части в виде g1(u)u , поскольку, вводя |
| (32) |
мы тем самым приходим к общей форме (31). Для нахождения решения уравнения (32) нет необходимости разбивать g (u) на два аддитивных члена, поскольку данная функция не зависит впрямую от временного параметра. Достаточно по аналогии с предыдущей задачей ввести квадрат комплексной единицы, а также добавить и вычесть первую производную от некоторой гладкой на интервале функции f (u) . При этом получим |
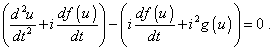 |
(33) |
Введенную в (33) производную от вспомогательной функции f (u) можно представить во второй левой скобке в виде |
| (34) |
Подставляя (34) в (33), приходим к выражению |
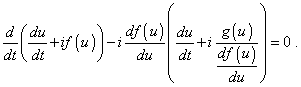 |
(35) |
Из (35) видно, что для идентичности выражений в скобках необходимо и достаточно, чтобы выполнялось равенство |
| (36) |
Интегрируя (36), получим |
| (37) |
Решение уравнения (36) обеспечивает нам нахождение первого частного решения основного уравнения (31), поскольку в соответствии с обоснованием методики в предыдущей задаче для этого достаточно, чтобы удовлетворялось равенство |
| (38) |
или |
| (39) |
которое при заданной по условию задачи зависимости g (u) уже интегрируемо. В частности, при переходе к линейному случаю, когда |
мы приходим к дифференциальному уравнению |
| (40) |
со стандартным решением |
| (41) |
Для нахождения второго частного решения, как и в предыдущей задаче, необходимо перегруппировать выражение (35), а именно |
 |
(42) |
При этом вспомогательное дифференциальное уравнение для f (u) будет тем же, но уравнение (38) изменится и примет вид |
| (43) |
или |
| (44) |
Сумма решений уравнений (39) и (44) дает общее решение дифференциального уравнения (31). В линейном случае решение, как и полагается, примет вид |
| (45) |
Но это не означает, что в общем случае решение уравнений (39) и (44) будет иметь вид столь тривиальных гармонических функций. Например, при |
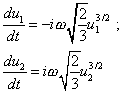 |
(46) |
решением данной системы уравнений будет выражение |
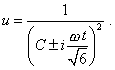 |
(47) |
В принципе, (47) не всегда может быть сведена к некоторой экспоненциальной комплексной функции. В частности, при начальном условии С = 0 |
| (48) |
4. Перспектива развития методики Проведенный поиск решений на двух характерных типах нелинейного волнового уравнения показывает, что представленная методика преобразований позволяет свести дифференциальное уравнение второго порядка к уравнению первого порядка, что существенно облегчает поиск решения задачи даже в случае, когда для интегрирования придётся использовать численные методы, не говоря уже о том, что во многих случаях появляется возможность получения аналитического решения, что было ранее невозможно. Но этим преимущества методики не ограничиваются и её успешное применение может быть расширено на достаточно широкий класс задач, близких к рассмотренным. В частности, если в первой, рассмотренной выше задаче кроме второй производной и свободного члена в уравнение будет входить первая производная типа q (t) du/dt , как правило, определяющая в физических задачах диссипативные процессы, то решение может быть найдено при следующей перегруппировке членов исходного дифференциального уравнения: |
 |
(49) |
Аналогично, если во второй, рассмотренной выше задаче будет дополнительно присутствовать первая производная типа q (u) du/dt , то решение следует искать при следующей группировке членов исходного дифференциального уравнения: |
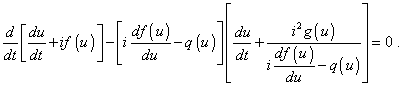 |
(50) |
Последнее уравнение приводит к дифференциальному уравнению первого порядка |
| (51) |
решение которого фактически определяет нахождение общего решения задачи. |
Литература: 1. Karavashkin, S.B. and Karavashkina, O.N. Investigation of elastic constraint non-linearity. IJMEE, 33 (2005), 2, 116- 133. |
Содержание: / 16 / 17 /