SELF |
36 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
36 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
Usually relativists violate the equivalence, parrying the criticism in a following way: “CRITIC. Just here the difficulty arises. According to the principle of relativity, the whole process has to go absolutely equally, if we express it in the frame K' which moves with the clock U 2 . In relation to the frame K' the clock U 1 moves ahead and back, while the clock U 2 is all time at rest… RELATIVIST. Your last statement is surely true, but the method of deduction is untrue, as, according to the special theory of relativity, the frames K and K' in no way are equivalent. Actually, this theory states the equivalence of only all Galilean (non-accelerated) coordinate systems, i.e. such coordinate systems in relation to which the material points isolated to a definite extent move rectilinearly and uniformly. Such coordinate system is, of course, the system K, not the system K' that is accelerated from time to time. So it is impossible to put forward any claims against the basis of theory of relativity, proceeding from the result that the clock U 2 after its motion ahead and back loses comparing the clock U 1” [22, p. 618]. None the less, despite the self-confidence of relativists, the claims exist and are considerable. First of all, as we could see above, the presence of physical time in both frames allows comparing the time intervals without the ahead/back motion, by way of arrangement of observers along the trajectory of clock motion with the exchange of information as a code, not as a visual observation of the clock arms. With the uniform motion of clock, even without synchronisation of origins of time intervals, after several sequential exchanges of such digital information, we will be quite able to judge of the pace of time flow in the moving frame. In this case no one, relativists in that number, can surely say which of the frames was accelerated before. It mostly is impossible to found, especially in solving problems like shown in Fig. 3. At the same time, if some speed exists between frames, anyway one of them or both some time ago were accelerated, – this means, the relativistic argument that frames identity is violated if one of them was previously accelerated and this is irrelevant to SR is illogical. If SR studies mutually moving frames and suggests some solutions concerning the formulas of coordinate and time transformation, in this way it admits dealing with the frames that were accelerated. It is of no importance, whether the frame returned either moved in one direction, – identity of inertial frames cannot change because of previous acceleration of one of them, or relativistic principle of relativity is untrue at all for any inertial moving frames. The more illogical are relativistic references to GR: “of course, we can fully clear up this issue only in frames of general theory of relativity” [23, p. 28]. If the fact of previous acceleration of an inertial frame that provided its speed with respect to other frame causes the violation of Einstein’s principle of relativity, Einstein would dismay proceeding from the principle of relativity when deriving his equations of frame-to-frame transformation: “With this aim (as the principle of constant speed of light with the relativity principle require) we have to express by equations the circumstance that the light, when it is measured in the moving frame, propagates also with the speed V” [7, p. 15]. Or even so: “In accordance with the relativity principle, the laws of nature have to be same in these frames, irrespectively of, are they at a relative rest either move uniformly and rectilinearly one in relation to another (footnote: Further we always will implicitly premise that the fact of putting in motion and stopping the ruler or the clock does not change the length of ruler or pace of clock)” [16, p. 152]. And saying of disturbed pace of clock, relativists always say of accelerated frame, while all external effects of acceleration and deceleration of the frame are fully identical and equally probable in absence of absolute frame. We always can find a third observer with respect to whom the initial frame moves with some speed, and a third frame accelerating from this second is decelerated. This last will mean the deceleration of the frame. With it, as relativists say, the speed lessening will cause higher, not lower pace of time. In particular, we have drawn the Reader’s attention to it when considered the twins paradox in [2]. None the less, basing exceptionally on their equations of between-frames transformation, relativists state that “things go otherwise in the theory of relativity. Consider an inertial frame K in relation to which the frame K' moves with the speed v in the positive direction of the axis x. In the frame K the first event occurs at the moment of time |
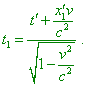 |
(11) |
The second event occurs at the moment |
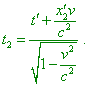 |
(12) |
Consequently, in K the events occur not simultaneously but when there passed the time interval |
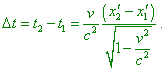 |
(13) |
Furthermore, dependently on the sign of (x'2 - x'1), the time interval If we now imagine from the view of this substantiation of relative simultaneity that just same result we will yield if exchange the frames, due to which the non-simultaneities of events will appear in the frame where we beforehand introduced the physical time, – the form of expression (13) will raise a natural thought: additional time intervals are caused not by non-simultaneity of events but by incorrect transformation that do not remain the physical time existing in each frame by definition after which the transformation was introduced. Anyway, this also is an important aspect to which we have to draw our attention in plotting and analysing the Minkowski diagram from the point of moving frame. |
Contents: / 28 / 29 / 30 / 31 / 32 / 33 / 34 / 35 / 36 / 37 / 38 / 39 / 40 / 41 / 42 /