V.6 No 1 |
39 |
| On correctness of basic postulates of SR | |
|
|
V.6 No 1 |
39 |
| On correctness of basic postulates of SR | |
|
|
So we see an ambiguity of time transformation when applying the Lorentz transformation. Outwardly in contradicts the before-established property keeping the inclination of generatrix in time. Factually such contradiction is caused by the fact that despite different degree of time transformation, the imaginary non-simultaneity between the rod ends does not depend on time, and the degree of lengths transformation is same. To show it, let us again look at the modelling equations (15) and (16). According to these equations, yield |
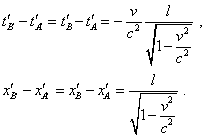 |
(25) |
Because of this independence of time and of spatial intervals of time, the generatrix inclination in the Minkowski diagram remains. Thus, we see that the Lorentz transformation disagrees with the conditions for which Einstein yielded it and violates the relativity principle when introducing the imaginary non-simultaneity and ambiguity of transformation of the time intervals that depend on the pattern of motion of the studied body. If we try to so-so match the Lorentz transformation with the conditions at which they have been derived, we can do it only introducing the correlation between the imaginary non-simultaneity of events to which this transformation brings us and the natural physical time of the moving frame. For it, for every point of the studied model we have from the values of absolute time that gives this transformation to subtract the difference between this time and physical time. Simpler speaking, we have to make a reverse oblique shear of the time for all points of the model, the oblique generatrix to become horizontal, which will evidence of the introduction of the synch physical time in the moving frame. Let us do so for our problem with two rods. First of all let us determine the inclination of generatrix to the spatial axis of the Minkowski diagram. We can make use of the yielded above values of coordinates (17) – for example, of the end B of the rod at the initial moment, although for this any other point or any other space-time interval like (25) of our model will work. For the chosen point, the relation will be as follows: |
| (26) |
We see from (26), this relation does not depend, as the above determined parameters did, on the choice of coordinates of the moving frame, and if not the ambiguity of absolute values of non-simultaneity, we could speak of relativity of simultaneity. But in presence of this ambiguity all talks of non-simultaneity of events are groundless. Noting (26), the expressions (15) and (16) will take the following form: for the ends of rod AB |
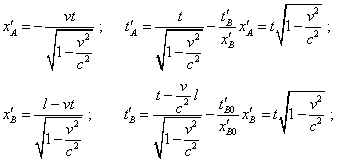 |
(27) |
and similarly for the rod A'B' : |
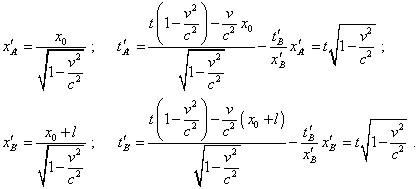 |
(28) |
As a result of subtraction made in (27) and (28), not only the time intervals of the ends of all rods gained the equal values but they became synch in full accordance with the statement of problem. To make sure, we can look at the diagram in Fig. 6 where we show the trajectories of rods in the moving frame with the introduced physical time. |
Fig. 6. Diagram of the trajectories of rods in the moving frame when the physical time was introduced in this frame. The parameters of diagram: l = 1010 m ; v = 0,8 c ; x0 = -1,5 l
|
If we disregard the proportional change of scale, this diagram factually coincides with the similar diagram which we can plot with the classical calculation. We see in this diagram that the simultaneity of coincidence of the rod ends which we saw in the stationary frame takes place in the moving frame, too. The generatrix also shifts strongly vertically, and during its motion all points of the trajectory shift, remaining their horizontal orientation. This evidences of the time synchronisation at all points of the studied model. And this is namely the graph that has to follow from the initial conditions (with exception of L-postulate) with the correct derivation of the Lorentz transformation. |
Contents: / 28 / 29 / 30 / 31 / 32 / 33 / 34 / 35 / 36 / 37 / 38 / 39 / 40 / 41 / 42 /