V.2 No 1

79

Some features of the forced vibrations modelling

Unfortunately, neither in practical studies (see e.g. [6], [16]) nor in the fundamental research on the basis of integral equations (see e.g. [11], [12]) this vibration regime is not considered and taken into account. “The solving of the boundary problems of the vibration theory is reduced, in the essence, to the calculation of eigenvalues caused by the natural frequencies or other parameters of the studied system and to the calculation of eigenfunctions (vibration forms). If the eigenvalues and eigenfunctions have been found, we can think the boundary problem solved... At present a great amount of approximate methods to calculate the eigenvalues has been developed, however they all are quite laborious, offer to find only the first eigenvalues and, the main, do not generalise the study of the systems with discrete and continuous mass distribution. So, as many authors correctly think, the eigenvalues calculus is up to now one of most important and laborious problems that many researchers are still involved in, in that number we can list Kellatz, Guld, Wilkinson in their lately published basic monographs devoted to the problems of natural vibrations. We can find the endeavours to establish the mathematical unification and synthesis of 1D discrete and continuous problems as long ago as in the works by Euler and Lagrange. However up to now setting up the analogies between such boundary problems is under process, for example, in the works by Krain, Atkinson and others” [11, pp. 3- 4].

In view of the new analytical method, we can figuratively explain the high-order eigenvalues problem, using the model consisting of three sections of elastically linked masses. If the first k₁ bodies have the element mass m₁, the second k₂  bodies have the mass m₂ > m₁ and the rest (n - k₁ - k₂) k₁ bodies - again m₁ , then, with the natural frequencies being undercritical for all sections, the eigenvalues of resonance frequencies transformed by the inter-affection of sections will relate to each section. At the frequencies overcritical for a ‘heavy’ section, the line will be definitively ‘divided’ into three sections. The first and third ones will remain the periodical vibration regime, and the second one - aperiodical. If the vibrations were free, we can expect the ‘partial’ resonances in each of three sections - in two at the undercritical band and in the third section - at the overcritical band. But if the vibrations are forced, the solution will depend on the external force application point.

So, describing the line by the unified matrix of general form and disregarding the possible transitions in some sections (or individual masses) to the aperiodical regime, we will naturally run into the insurmountable problems in describing the processes in a line. And the fact that neither matrix method nor integral equation method reveals the overcritical vibration regime evidences only some incompleteness of these methods and necessity to develop them with account of features of vibration process. The new non-matrix method can be useful in it, too. Some results yielded with it were presented in [1]- [3], and the solutions analysed in this paper have been yielded also by this method.

3. Effect of the external force application point

3.1. Free-ends finite line

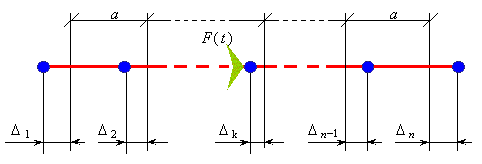
To make convenient the comparison with solutions presented in [2], consider a finite free-ends line whose kth element (1 k n )  an external harmonic force affects. The general form of such line is given in Fig. 1.

Fig. 1. General appearance of a finite elastic line whose kth element is affected by an external force

The modelling system of equations has the form

where F(t) = F₀ is the external force affecting the kth element of the line, m is the mass of the line element, s is the constraints stiffness coefficient and _i is the momentary shift of the ith element from the state of rest.