V.2 No 1 |
57 |
|
On complex resonance vibration
systems calculation |
||
|
||
Basing
on |
||
|
(20) |
|
where a
is the distance between the elastic line non-excited elements, and |
||
|
||
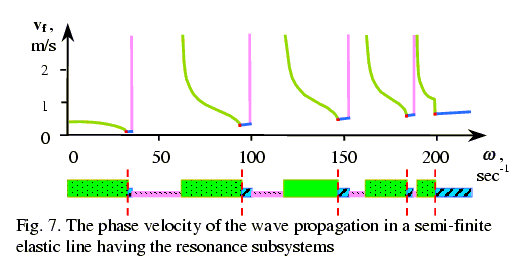
We can
see from Fig. 7 and (20) that in the complex aperiodical regime the phase velocity turns
to infinity, as at these bands Going
on analysing (20), we see that the phase velocity achieves its minimal value in
aperiodical regime, since at these bands Furthermore,
it is typical that despite the sections having negative measure of inertia appear, the
transfer function phase retains delaying always, and this also is in full accordance with
the above Skudrzyk’s statement [1] that the negative measure of inertia of line
elements fully corresponds to the conservation laws. This
negative measure of inertia, which we used to think strongly associated with the mass,
does not mean a negative mass introduction. In this case, there reacts not a separate mass
but a complex system of elastically connected masses being the parts of a general elastic
system. So we have to identify just this reaction with the negative measure of inertia of
the subsystem. We see that the pattern of subsystem reaction to the external action
changes. With it the pattern of process also changes. And the phase with regard to the
external action retains negative. Thus, introducing the idea of negative measure of
inertia, we do not contradict the laws by Newton who considered an accelerated body as an
entire rigid system. |
||
Contents: / 48 / 49 / 50 / 51 / 52 / 53 / 54 / 55 / 56 / 57 / 58 / 59 /