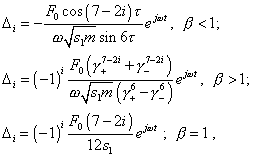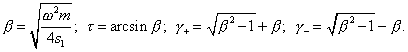non-linearity31

V.2 No 2	31
Investigation of elastic constraint non-linearity

3. Solution seeking technique In order to identify the way of seeking the solution for (3), note that in case s₃ = 0 this system reduces automatically to that linear whose solutions we know [10]:
	(6)
where i = 1, 2, 3 ,
	(7)
This gives us a possibility to seek exact analytical solutions for each separate harmonic in a simple way; when seeking the solution, we will explain the features of this way for each step corresponding to the seeking of a particular harmonic. In order to determine the direction of step-by-step finding the harmonics, let us draw our attention to the following detail. If we substitute, e.g., the periodical solution (at < 1) from (6) into the general system (3) at s₃ 0, then on the right-hand part of each equality an additional summand corresponding to the third harmonic will appear and violate the correspondence of (6) to (3). If we try to take into account the appeared additional harmonic, then in substituting the refined solutions to (3) there will appear the terms of the next, higher harmonics, etc. This corroborates the known fact that "due to the presence of nonlinear terms, in the solution of forced vibration equation, the harmonics with the frequencies approximately equal to n₀ will be inserted" [4, p. 314]. This feature gives us the reason to seek the general solution as a series beginning with the fundamental harmonic corresponding to the external force frequency
	(8)
where _ip is the yet unknown momentary shift of the i th element of an elastic line (in this problem i = 1, 2, 3) corresponding to the pth harmonic of a nonlinear dynamical process. As we see, the absence of the condition of non-linearity smallness in the elastic constraints has led us to the essential change of the form of the sought solution. In particular, the parameter _ip in (8) has neither direct nor reciprocal power-type dependence being typical for asymptotic techniques (see, e.g., [19, p. 45]), the same as the parameter indicating, for example, the smallness of function Q (in comparison with the linear term) used in the Krylov-Bogolyubov technique [4, p. 314] in solving the problems of the kind
	(9)
By its shape, (8) looks more like an expansion of a complex function into the Fourier series that usually is inapplicable in solving the nonlinear mechanic problems by the conventional methods. But with it the summation in (8) is carried out only in the positive values of p, and even the zero term is absent. Should we actually seek the solution in the form of Fourier expansion, we would not may narrow the summation region without limiting the generality of the solution. However, as we will show below, the coefficients _ip are the resonance-type analytical functions depending on the parameters of the studied elastic line and external force frequency . And each coefficient of (8) will be the solution of its own system of algebraic equations; therefore it will have its own functional dependence. At the same time we know (see, e.g., [20, p. 214] or [21, p. 143]) that in the expansion into Fourier series
	(10)
the coefficients a_k and b_k are real numbers, and the coefficients c_k are complex numbers that are determined from the equality
	(11)