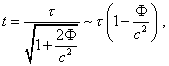absolute03

V.3 No 1	3
Notice on physical Absolute

We can conclude the same relatively the other relativistic experiments, in that number their gedanken experiments. Let us take for example the known Einstein's clock paradox. This gedanken experiment has been multiply discussed in the literature of different scientific level. We can find in [13] a good bibliography and description of all objections concerned to this paradox. Despite all attempts to persuade themselves and the surrounding people that there is no paradox, the relativists never presented a cogent proof. If we stand strong on the Mach's position, then, as the vehicle stops accelerating, the inertial systems of twins should become again fully identical, and time deceleration has to be pure fictitious and dependent on the used technique of checking the clocks. Actually, if we use the favourite relativistic technique and check the clocks by fixing the intervals of light travelling in the checked reference frames, there will be a difference, as it follows also from the Galilee's transform. But we should not forget that the twins paradox considers not the simultaneity of events, but only the flowing time velocity. So, proceeding from the reference frames equivalence introduced by Einstein - "The relativity principle requires, the full coincidence of laws to be extended also to the case when S ' moves evenly and rectilinearly as to S . In particular, the light velocity in the void has to be expressed in one and the same number" [Einstein: 14, item 3, p. 70- 71], - we can, doing not exceeding the limits of SR, construct the technique of strong synchronisation of the time flow. It would be sufficient for it to use the fact that, according just to Einstein, between-the-frames transformation formulas have a definite reversibility; it is expressed in the fact that if we had a standard system of transformation between the moving (marked by the dots) reference frame and stationary (non-dotted) frame, then, "solving the relationships with respect to x, y, z, t , we can easy yield the relationships having the only difference that the 'primed' values in them have been substituted by those 'non-primed' and vice versa, and there is - v instead v . This follows immediately from the fact that the system S moves evenly with respect to S ' in the direction x' with the velocity - v " [Einstein: 14, item 3, p. 73]. So, by the Einstein's calculations, we can infer that if both twins have some clocks going with the frequency f₀ , then for each twin the frequency of clock of his brother will be
	(5)
"… in other words, the clock moving as to some reference frame with the velocity v goes in this system slower as [1 - (v^²/c^²)] ^{^-1/2} than the same clock in case when it is at rest as to the same frame" [Einstein: 14, item 4, p. 74]. Thus, the difference of frequencies will be
	(6)
and, taking into account the above, in limits of SR this difference has to be detected similarly by both brothers. Hence, if both twins maintain the equal difference of frequencies (6) and the frequency of their clock, regularly informing each other of the values of these parameters for the correction, we can surely state that the flow of time in both frames will be fully synchronised, as in (6) other regularities are absent, and the velocity of mutual motion of the frames is the same! Given also the intervals of even motion of the vehicle well exceed the intervals of accelerated motion and, dependently on the task, can be chosen unlimitedly large (at least theoretically), the astronaut's general oldening should not obey the regularity of the total time of travel, as Einstein's relativistic conception predicted. Just this problem made the relativists to assign the twins' frames non-identical, having violated in this way both the Mach's relativity principle and that Einstein's on whose basis he postulated the constant velocity of light in all reference frames: "To describe, what follows from this in the view of one and another twin, we have to exceed the limits of SR and apply to GR which gives the sequential method to consider also the state of accelerated motion. None the less, SR gives us the 'true answer', if the phenomenon is described in the inertial frame; in such frame the brother who stayed home appears older than his travelling brother" [Panovsky: 15, p. 208- 209]. Additionally, let us look at the construct of Panovsky's citation. This is the typical relativistic style - to divert the reader's attention from the problem. He first claims that this problem is solved with GR, out of frames of SR, perfectly understanding that the intervals of acceleration cannot seriously affect the time deceleration, because they are not long. Then he adds, the problem is also solved in frames of SR which the relativists have to leave to solve the paradox. However the paradox is unsolvable in frames of GR too, and this is also easy to show. To prove it, consider the problem of not two but three observers A, B and C ; two of them are the twins we know, and they do not know of the third observer C (a favourite argument of relativists - to limit the observer's scope), but he watches them in order to check the velocity of time flow. Let the events occur in usual way. The twin A is preparing to the flight and checking his clock with the observer B . After that A starts with the acceleration a and during some time t₁ achieves the velocity comparable with the velocity of light (assume, v = 0,5 c ). As we cited above, the relativists are sure that taking into account this interval of the astronaut's travel will completely explain the clock paradox. Let the clock frequency in this interval vary after the relativistic conception. Then, according to Einstein, "If the radiation emitted in the evenly accelerated reference frame K ' in S₂ towards S₁ had the frequency f₂ relatively the clock being in S₂, then, when arriving to S₁, it has, relatively the alike clock being there, the frequency, equal already not to f₂ but to a larger frequency f₁ which in the first-order approach is equal to
"	(7)
where is the acceleration in the gravity field, h is the distance between S₂ and S₁) [16, p. 170]. On the basis of this expression, Pauli has obtained the regularity that gives the relationship between the time in the accelerating frame t and the time of stationary observer [Pauli: 12, item 53, p.221]:
	(8)
where = h is the gravity potential equivalent to the acceleration of the clock of twin A. "The equation (8) has the following physical meaning. If we put one of two alike and initially synchronous clocks for some time into a gravitation field, after this the devices will not go synchronously, on the contrary, the clock which was in the gravitation field will lose. As Einstein [17] indicated, this is the basis to explain also … the clock paradox" [Pauli: 12, p. 221- 222]. Possibly, such interpretation of the paradox might be admissible, if not two principally important points. First, (8) does not correlate with the following formula of deceleration in SR:
	(9)
The difference is essential and can be got over only at small velocities, while the relativists use (9) to explain the time deceleration for the relativistic particles. Second and the main, the time deceleration in (8) is true only in the interval of accelerated motion. When this time interval is over, the potential has to vanish, otherwise the acceleration process will remain. But as we can see from (8), when the potential vanishes, the difference between the time flow in the twins' frames disappear. Thus, even if the velocity of time flow changes in accordance with GR, this will be confined only to the short intervals of accelerated motion. As we can choose the intervals of even motion arbitrarily, there will be no correspondence between the calculations made with SR and GR. Consequently, the above Panovsky's statement "None the less, SR gives us the 'true answer', if the phenomenon is described in the inertial frame" [Panovsky: 15] is incorrect.