SELF |
4 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
4 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
Let us consider two reference frames, in each there is a clock of the same construction which we can adjust. We do not know for certain, whether the light speed is constant in transition from one frame to another. Note, this statement of problem satisfies both Einsteinian Relativity and those conceptions which you think more perfect. We have to determine the conditions of timing. This model is shown in Fig. 1.
|
|
Fig. 1. Model for timing in mutually moving inertial frames
|
In this figure we see the primed movable frame and
non-primed stationary one. The clocks are marked as periodic structures. They have a
feature - the pulse is sent from the stationary frame to that movable exactly at the point
1 and is received also at the exactly determined point 1'. Thus, the timing pulses with
some timing frequency come from the stationary frame to that movable. To synchronise, we
are interesting first of all in transformation of timing pulses when receiving by movable
observer. Naturally, in accordance with Doppler effect, in the movable frame, the time
interval will some increase if the movable frame runs from that stationary, and decrease
if the movable frame runs closer to that stationary. On one hand, as Einstein thought,
this is an inconvenience, as the measure of time intervals extension depends on mutual
position of frames. But on the other hand, this is an invaluable advantage, as this allows
the observers to be informed about interrelation of processes occurring within these
frames. Actually, if the observers once have timed their clocks, the difference in periods
will depend on time necessary to pass the distance 1 - 1'. But if, going on moving
relatively each other, the observers repeat their experiments, they will see the time
delay between the timing pulses changed. This, to the point, fully contradicts the
conclusions of Einstein's mathematical formalism, though this is just the reality which
you are proposing to consider in the beginning of your post. Actually, if the frames are
moving in parallel and their axes x are distanced by some value d, and if
there is some angle
|
|
Fig. 2. The diagram helping to calculate the pulses broadening
|
 |
(17) |
| and |
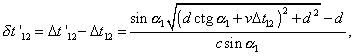 |
(18) |
| where |
| (19) |
| the regularity with respect to the angle
|
|
Fig. 3. Plots of relative variation of time interval of timing pulse (continuous lines) and derivative of received timing pulse with respect to the instantaneous angle between the stationary and moving frames (dotted lines), with respect to the between-frames angle and distance |
| In Fig. 3 we first of all can see that at any d the
curves of relative variation of time interval go through zero point. This means, there
exists an interposition at which the difference of time intervals is zero. At small
distances this zero point is shifted from the position of between-frames vertical line,
but at distances about 30 light seconds and more this point can be strongly fixed on the
vertical between the directions of observers' motion. In addition, at large between-frames
distance the derivative (denoted as a dotted line of the same colour as the curve) becomes
strongly symmetrical as to the position of the vertical and has the minimum there; and
that minimum coincides with the zero point of the relative difference of time intervals.
Note also, we calculated the curves for quite large speed of moving observer, for whom 30
light seconds is quite small value.
On the basis of this regularity we can see more clear the technique of timing. To time, the moving observer need not to know the law of light velocity transformation. Whatever it can be, the minimum of derivative will not change its position. And at that minimum the time intervals will remain EQUAL. To register this minimum, the moving observer has only to copy with the necessary accuracy the transformation law of time interval of timing pulses received from the stationary observer and to re-calculate it relatively the zero point of relative difference. As the moving observer cannot experimentally obtain the relative difference per se, he can seek the extreme point by variation of the derivative of experimental data. At large between-frames distance the moving observer can obtain these data immediately, and at small distance he can create a probe frame, if sending it with the copy of clock far from the stationary observer. This will enable him to avoid the shift of extreme observed at small distances between the frames. As we see, the inconvenient reference frame just enables us with any given experimental accuracy to synchronise the time in frames without any additional premises and transformations. If well-made timing, the time intervals in both frames will be equal with the given experimental accuracy quite enough for relative results of practice. Of course, the researcher will need to complete the curves to obtain the synchronous interval, but this is an usual experimental situation. As an example we can mention the calculated value of absolute zero of temperature which no one achieved, but the value has been calculated with high accuracy (-273,16o C). And we have to pay our attention that in the region of extreme the curve of derivative is very smooth - this considerably lessens the error connected with the inexactly found point of extreme. This feature is just reflected in the fact that the sidereal time is most precise. As is known, "when observed on passage instruments and zenithal tubes, there is applied the method to register the instants when stars passing the meridian. If observed on prismatic astrolabe by Danjon, there are registered the instants of stars passing through the al mukantarath (small circle of celestial sphere parallel to the horizon) with zenithal distance of 30o. After preliminary data, the errors characterising the accuracy of time determination with the help of these instruments are equal, accordingly, to 19, 18, 16 and 12 msec" [Citovich, A.P. Time. Physical encyclopaedia, v. 1, p. 333]. With this technique of timing, we can obtain even more
accurate time, synchronising it with the average statistic intervals of pulsing of a dozen
most stable cepheids. The very stability of cepheids will tell us not only that the
processes in them are stable, but that we are positioned as to them in the region of
extreme. So the time measured in such way will be most close to the Newton's absolute
time. It follows from this that if two observers in mutually moving inertial frames
synchronise their clocks not with each other, as Einstein suggested, but in accordance
with Newtonian mechanics with the absolute time after the same far cepheids, they both
will have a common time standard with quite good experimental accuracy. And having it,
they will easily check the simultaneity of events. And we can notice one more merit of this technique "inconvenient" for relativists. When plotting the curves of time intervals variation, the moving observer does not need to use the clock timed with the stationary observer. To measure this regularity, he will need some strongly periodic process in HIS own frame in whose units he can plot. And having it plotted, he can calculate the point of extreme and take as the standard the value of his own periodic processes that corresponds to the calculation. Well, we do not surprise taking as the unit of length 1 650 763,73 of radiation period corresponding to 2p10 - 5d5 transition of crypton-86 atom (even with hundredths!) And so in this case. In this technique the metrological nuances can be very different. In particular, instead mechanical pendulums one can synchronise with the help of light pulsing packets generated on a device like shown in Fig. 4.
|
|
Fig. 4. Device to generate the packets of synchronous pulses |
We see this device much alike one of popular constructions of Rojdestvensky's interferometer, but it has some difference. Not continuous radiation of source but synchronous pulses of large relative pulse duration is fed to the input of this generator. A part of light beam is immediately reflected from the semi-opaque mirror to the output of device, and a half of beam sequentially reflects from internal mirrors and also appears at the output, some shifted in time as to the first half. This creates packets of pair pulses which can be transmitted by the stationary observer. The time delay can be easily regulated by the distance between the internal mirrors; as stationary as moving observer can regulate on his instruments when correcting the time interval. As we see, the clock timing problem is difficult (as many
things in the issues of metrological standards) but quite realisable. With it, all clocks
in the inertial frame are timed equally without any transformation of the time unit. The
only thing is needed - observers to be just observers, not Einstein's guinea-pigs. We regret much saying it, but this is so. All the best to you, Sergey and Olga Karavashkin 18.12.2004 |