V.6 No 1 |
3 |
| On excited state of orbital electron | |
|
|
V.6 No 1 |
3 |
| On excited state of orbital electron | |
|
|
Even more free interpretation we see in ‘composing’ the phenomenologies of solutions of the Schroedinger equation. For example, Fermi builds his basic equation with the following logic [8]. To begin with, he draws an analogy in optics and mechanics, or rather in Mopertui principle and Fermat principle on whose basis he derives the formula for the group velocity (Lecture 1) |
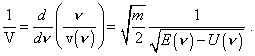 |
(7) |
It is easy to see, here he based fully on classical physics and (7) reflects this important circumstance. Should he begin with the Heisenberg principle, it would be simply impossible for the models to which he intended to apply his results. Then Fermi writes: “Introduce the notation |
| (8) |
then |
| (9) |
[8, p. 19]. But this expression also has been carried over from wave physics. In particular, Shpolsky [9] showed it: “To calculate the related expression for the classical frequency, let us take the case of linear harmonic oscillator. The energy of oscillator is |
from which |
The integral of action will be in such case |
| (10) |
Considering the energy E as a continually varying parameter, find the derivative |
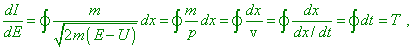 |
(11) |
where T is the oscillation period. From it we yield the following significant expression for the classical frequency: |
| (12) |
We can show that (11) has to take place for any periodical systems with one degree of freedom… Comparing (12) and (8), we come to the following result. Both in classical and in quantum theory the frequency can be calculated as a relation of the energy increment to the action increment, but, while in the first case we take infinitesimal increments, in this second we have to take finite differences” [9, p. 360–361]. Thus we see, the very idea of the Planck constant also
results from classical wave physics. The only difference - the degree of discretisation
shown by Shpolsky - is only the feature of model of electron’s periodic motion in the
atom. Let us recall, in the statement of problem of orbital electron excitation, Bohr
introduced a stipulation: “Now assume that the electron emits a
monochromatic radiation with the frequency “There is a far-going analogy of the quantum-mechanic problem |
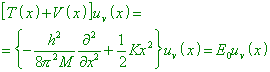 |
(13) |
and of the classical problem with the energy |
| (14) |
(where T (x) is the
kinetic energy corresponding to the operator T (x), and
p = Mx conjugate to the operator p = (h/2 |
| (15) |
So the frequencies of main oscillations of multiatomic molecules can be calculated classically” [13, p. 15]. It follows from this that Fermi was not so much mistaken when integrated (11), taking I as a constant value equal to h. But from this it also follows that the idea included in the Planck constant has the classical nature determined by the resonance pattern of the orbital electron’s motion. |
Contents: / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11 / 12 / 13 / 14 / 15 /