V.6 No 1 |
47 |
| On the wave-particle duality | |
|
|
V.6 No 1 |
47 |
| On the wave-particle duality | |
|
|
To show it, let us go on considering Born’s model. We
stopped at the point that after Born’s idea, the atomic field only scatters the wave
but does not change its phase. “In this case the wave scattered by the atom in direction OR under an
angle |
| (7) |
where f (sin
|
|
Fig. 10. The scheme of electron’s interaction with a separate atom (after Born). The exponential term (top, left) factually determines the longitudinal electron wave running on the atom and the stationary appearance of the wave function of atom
|
In its turn, as we know, the atomic amplitude directly
depends on the form-factor F ( Or rather, “in case of scattering of quite fast electrons, we
yield the following expression for the number of particles deflected by the angle |
| (8) |
where |
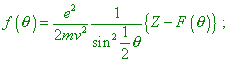 |
(9) |
this is reduced to the Rutherford formula
…, if neglecting the term F ( “Observation F ( |
| (10) |
Although mathematically it is simple – we have only to invert a usual Fourier integral, – to do so practically is an extremely complicated task. The matter is, we have to study not separate atoms but assemblages of their giant quantities in gases, liquids or solids. The structure of the medium causes interference patterns superimposed on the patterns related to the form-factor. In gases and liquids whose atoms are chaotic we yield the rings of decreasing intensity around the falling ray. The appearance of rings depends mainly on the average distance between atoms. In solid crystals we yield the well known Laue – Bragg interference patterns. The form-factor modifies the intensity distribution in these effects, but not only it affects. There are mere geometrical factors – such as the width and distance from the used splits, temperature effect related to the thermal motion of atoms, crystal non-ideality etc. So it is not so easy to separate the form-factor effect from the affection of all other causes that produce the observed intensity” [2, p. 225]. This citation from Born shows that after his own opinion,
the form-factor, although it takes some part in the electron diffraction, is not
definitive, though in the Born’s approximation of interaction of electron with a
separate atom the structure of continuum is disregarded, consideration is reduced to the
interaction of electron de Broglie wave with the potential of atom. Born [2, p. 226] and
his interpreters [6, lecture 26], [8, chapter XVII, section 137], [9, part I, section 14]
etc. show the same approach to this approximation. “In
collision with atom, we have to account also the wave functions describing the interior
structure of atom. In elastic scattering the state of atom does not change. So Up'p
(the matrix element of interaction energy with respect to the wave functions of
free particle before and after collision – Authors) has to be
determined as the matrix element with respect to wave functions The equation for the correction |
| (11) |
(U is the potential energy). As we know from electrodynamics, the solution of this equation can be written in the form of ‘lagging potentials’, i.e. as |
| (12) |
[8, p. 189]. Note that in (12), in full accordance with the statement
of problem, the potential function that includes the electron cloud of atom screening the
charge of nucleus is stationary. Actually, “Denoting the density of charge distribution in the
atom through |
| (13) |
The sought matrix element Up'p is, mainly (! – Authors), the Fourier
component of U (i.e. of |
| (14) |
where en (r) is
the density of electron charge in the atom. Multiplying by |
| (15) |
Thus, yield for the integral of our interest the expression |
| (16) |
where the value F (q) is determined by the formula |
| (17) |
and is called the atomic form-factor. It is the function of the scattering angle and of the speed of falling electron” [8, p. 614]. With it, “Note that same problem can be solved also after the stationary theory of excitations, as the potential energy of interaction does not depend on time” [9, p. 204]. Thus, we clearly see that the conventional quantum-mechanical solution is based on the reason that the electron, being on one hand a particle, has the statistical de Broglie distribution before the interaction with an atom. After the excitation theory, the first and next approximation is known to be well less than the non-excited state – the distribution function of non-excited electron. The authors omit it and do not substantiate the physical causation of interaction of the wave function of electron with the stationary field of atom and the very essence, how the de Broglie wave is formed with the specific vector k = kn, while in words they say of continuous spectrum of this statistical wave function. In the last case, should the initial state contain a continuous spectrum, the difference [8, p. 555] |
| (18) |
would be also a continuous, not discrete spectrum, and the whole problem of merely formal substantiation of the discrete function as a consequence of interaction with an atom would be invalid. Thereupon there will appear not the diffraction pattern but some conventional version of Rutherford’s scattering, which caused so many essential reservations of Born. |
Contents: / 43 / 44 / 45 / 46 / 47 / 48 / 49 / 50 / 51 / 52 /