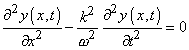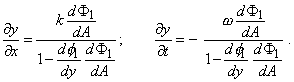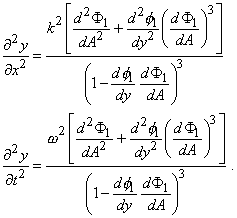т.6 No 4, сс 13 - 19

15

Особенности воздействия наклонной силы

Из проведенного исследования видно, что наклонные колебания далеко не всегда возникают вследствие нелинейных процессов в упругой системе, как это предполагалось до сих пор. Наклонные волны вполне естественным образом способны возникать при воздействии на упругую систему силы, наклонной к направлению распространения волнового процесса. И этот вывод может быть достаточно просто распространен на самый широкий спектр колебательных процессов.

3. Траектория движения элементов линии

Если обратить внимание на траекторию движения отдельного элемента исследуемой линии, то несложно установить, что эта траектория имеет вид эллипса, описанного вокруг точки покоя элемента. Наклон же волны формируется за счет фазы смещения движений по данным эллиптическим траекториям от элемента к элементу. Приведенная структура колебаний в физике достаточно хорошо известна, в частности, в волновых процессах в неограниченных объемах жидкости. “В волне движение жидкости не стационарно. Поэтому пути отдельных частиц во времени вовсе не совпадают с линиями тока. Они имеют совершенно другой вид. При небольших амплитудах они с большим приближением являются окружностями. Эти круговые пути мы находим как на поверхности, так и в глубине жидкости. Только в самых верхних слоях диаметры круговых путей наибольшие” [4, с. 300- 301].

Конечно, колебательные процессы в объеме имеют свои особенности. Тем не менее характерно, что основополагающие закономерности прослеживаются уже в одномерной модели. Из полученных решений также следует, что эллипсоидальный характер колебаний элементов сохранится и в критическом, и в апериодическом режимах. В последнем случае вследствие этого в линии формируется сложная быстрозатухающая вдоль линии волна, что является еще одной особенностью, которую демонстрируют точные аналитические решения.

4. О новом классе функций, являющихся решением волнового уравнения

Вышерассмотренные обобщения можно распространить и на решение волнового уравнения в целом.

Известно, что дифференциальное уравнение гиперболического типа

где c = /k - скорость распространения волны, т.е. решение в виде двух явных функций от (x - ct) и (x + ct) соответственно.

Данное решение считалось до сих пор единственным и полным, что обусловлено теоремой о единственности решения дифференциального уравнения. Тем не менее, существует еще один класс функций, не учитываемый решением (13), являющийся решением дифференциального уравнения (12). Общий вид данного класса функций может быть представлен в следующей форме:

где ₁(y) , ₂(y) - некоторые дважды дифференцируемые функции. Иными словами, приведенное решение (14) относится к классу неявных функций, закономерности поведения и способы дифференцирования и интегрирования которых существенно отличаются от поведения и способов оперирования с явными функциями. Существенно, что если для явных функций создана определенная систематика дифференциальных уравнений и для определенного класса этих уравнений определены закономерности и схемы нахождения решений, то для неявных функций всех этих наработок нет. И вполне естественно, что соответствие выражения (14) дифференциальному уравнению (12) можно в настоящее время проверить только самым простым способом – прямой подстановкой (14) в (12).

Для этого на основании известных законов дифференцирования неявных функций найдем первые и вторые частные производные по x и t от выражения (14). Для упрощения выкладок будем рассматривать половину правой части выражения (14)

где

Первые производные имеют вид:

Вторые производные после преобразования и подстановки выражений (16) приобретут вид

Подставляя (17) в (12), получим требуемое. Аналогично можно доказать соответствие и второй части выражения (14) уравнению (12).