1

Теорема о роторе потенциального вектора

Теорема о роторе потенциального вектора

в динамических полях

О.Н. Каравашкина, С.Б. Каравашкин

Специализированная лаборатория фундаментальных исследований СЕЛФ

Тел.: +38 057 7370624

e-mail: selftrans@yandex.ru , selflab@mail.ru

Abstract

В статье проведено исследование циркуляции и ротора потенциального вектора в динамических полях. Доказана теорема о том, что в динамических полях ротор потенциального вектора пропорционален векторному произведению единичного вектора направления потока на производную от вектора потока по времени. При этом потенциальный характер вектора не нарушается, поскольку циркуляция обусловлена конечностью скорости распространения волны в пространстве. Рассмотрены приложения к акустическим и электромагнитным полям. Приведены результаты экспериментального исследования поперечной акустической волны в воздухе, подтверждающие возможность формирования поперечной волны путём линейной суперпозиции потенциальных динамических полей.

Ключевые слова: теоретическая физика, математическая физика, волновая физика, векторная алгебра, акустика, теория электромагнетизма, динамические потенциальные поля.

1. Введение

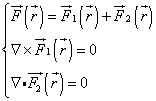
Одним из основных свойств векторных полей является то, что “если дивергенция и ротор поля () определены в каждой точке () области V, то всюду в V функция () может быть представлена в виде суммы безвихревого поля ₁() и соленоидального поля ₂():

(Теорема разложения Гельмгольца)” [1, стр.173].

Можно сказать, что уравнение

“является достаточным условием для консервативного поля, т.е. для того, чтобы поле можно было описать градиентом некоторой потенциальной функции” [2, с. 89]. Иными словами, если вектор () является потенциальным, то в исследуемой области, безусловно, выполняется равенство (2).

Обращает на себя внимание тот факт, что определение ротора вектора и существующая теорема о роторе вектора сформулированы для стационарных полей, в которых вектор зависит только от координат, но не от времени. В этом легко убедиться, обратив внимание на аргумент, от которого зависит вектор () в стандартном определении и теореме о роторе вектора. В частности, в теореме Стокса: “Если векторная функция () однозначна и имеет непрерывные частные производные всюду в конечной поверхностно-односвязной области V₁ и если лежащая в области V₁ поверхность S односвязна, непрерывна и ограничена регулярной замкнутой кривой C, то

т.е. криволинейный интеграл от () по замкнутому контуру C равен потоку вектора () через поверхность, натянутую на контур C”[1, с.171].

Обычно указанное определение потенциальности распространяется и на динамические поля, в том числе и на сложные акустические поля в газовой среде.

Как известно, “в жидкостях и газах не существует упругого сопротивления поперечным смещениям частиц, но лишь изменению объёма, т.е. сжатию или разрежению. Поэтому в таких веществах могут распространяться только продольные волны” [3, с.114]. “Таким образом, в векторной форме имеем:

(где – скорость смещения молекул элементарного газового объёма, – акустический потенциал), т.е. теорему Стокса: ротор градиента тождественно равен нулю. Следовательно, метод потенциала скорости применим только для безвихревых движений. Но акустическое движение в жидкости и газах всегда остаётся безвихревым, даже если учитывать эффект вязкости. Можно показать, что вблизи твёрдой границы всегда существует вихревой слой, но этот граничный слой чрезвычайно тонок” [4, с. 392].