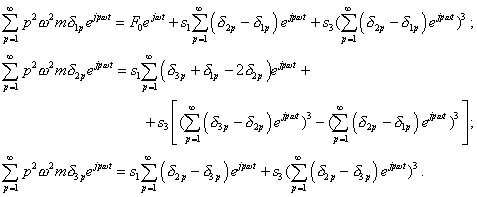32

S.B. Karavashkin and O.N. Karavashkina

In other words, the form of solution (8) differs from the form of Fourier expansion, so that it is a functional series that is formed as a result of sequential compensation of higher harmonics that arise in the system of equations with the non-linearity. Proceeding from the fact that expansion of stiffness coefficient (1) contains only the growing powers of , the series-type solution beginning with the fundamental harmonic of affecting force (i.e., with p 1) will completely describe the entire spectrum of harmonics arising in a nonlinear elastic line as a result of action of a pure harmonic force.

Of course, if the expansion (1) had some other form - for example,

then, following the chosen way, we would have to seek the solution in some other form that would allow to find the solution for an elastic system with a non-linear constraint of the type (12). However, since the expansion (12) is far beside the frames of our investigation, in the meantime we will confine ourselves to the class of non-linearities described by the expansion (1); in this way we will additionally emphasise the forms diversity of the non-linear dynamic problems and corresponding diversity of approaches to their solving. The studying of the solutions of nonlinear problems on the basis of expansion with the help of Volterra series similar to (12) can be found in the book by Wilson J. Rugh [22]. True, the condition of smallness of the model nonlinearity which we can neglect in our approach retains in that case.

As a consequence of the above, the convergence of (8) will determine not the admittance of expansion _i in harmonics pt, as it would take place in case of expansion _i into Fourier series; it will indicate the existence of a finite solution in one or other region of the range. Thus the convergence of (8) will in fact determine the vibration stability at the studied band.

Proceeding from the above analysis, the technique to find the solution of nonlinear system of equations (3)- (4) can be determined as a sequential compensation of the residual terms of the higher harmonics when substituting the expansion (8) into this system of equations. For it, we will substitute (8) into (3) and sequentially select the terms of corresponding harmonics, basing on the fact that (3) can be identically zero only in case if the corresponding equations for all harmonics are zero.

As we can see, due to this substitution the modelling system (3) has gained the known form of the ensemble of equalities of harmonic components. So, as we said it above, this system identically vanishes only with the equality of related coefficients for all harmonics.

To select the corresponding harmonics, we could make use of the orthogonality of the system of functions , p = 1, 2, 3, ... (see, e.g., [20, p. 213]) and time independence of _ip, applying to (13) the operation similar to the convolution usually used in selecting the Fourier harmonics. Since  _ip are some analytical functions which can turn into infinity at the resonance frequencies, the substantiation of convolution applicability in this case will be incomplete. However in systems of the type (13) there is no direct necessity to apply the convolution to select the harmonic components. It is sufficient to equalise to zero the coefficients at the corresponding harmonics in each equality of this system of algebraic equations. With this approach, the resonance pattern of the coefficients _ip will be of inessential importance, if the coefficients of related harmonics in each equality of (13) in the aggregate are identically zero.