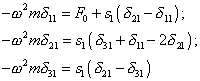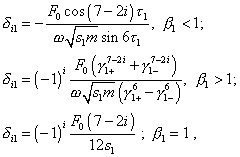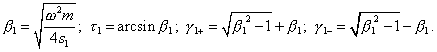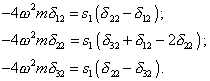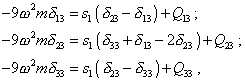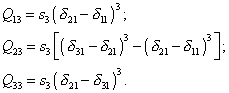non-linearity33

V.2 No 2	33
Investigation of elastic constraint non-linearity

Using this standard algebraic technique to select the harmonics, consider sequentially the systems of equations in (13) for each harmonic separately. For the first harmonic (at p = 1) the strictly linear system of equations
	(14)
is formed. We already know its solutions, as they are similar to (6):
	(15)
where i = 1, 2, 3 ,
	(16)
Note that in nonlinear dynamics all three vibration regimes remain for the first harmonic, and the boundary frequency ₀₁ also corresponds to the linear vibration regime:
	(17)
The system of equations for the second harmonic is the following:
	(18)
This system is also linear and relates to free vibrations in an elastic line with the stiffness s₁. We can see from (18) that in case where the affecting force F(t) does not have the second harmonic, and/or the stiffness coefficient does not have a square term of the expansion, and/or the free vibrations are absent in the system by the statement of problem, the equality
	(19)
is true. However this result is not general. If any of the above conditions was violated (not only the square term in expansion in the powers of the stiffness coefficient is absent, as it is conventional), the second harmonic is present in the nonlinear dynamical process, causing the hysteresis in the vibration pattern. It is desirable to take this feature into account in solving the problems of nonlinear dynamics. The system of equations for the third harmonic can be written as
	(20)
where
	(21)
As we already know all values _i1 involved in Q_i3, (20) is also reduced to the linear system describing the vibrations in an elastic line with the stiffness s₁ (the same as for the first harmonic). The nonlinear coefficient s₃ itself determines the amplitude of equivalent forces Q_i3 affecting the corresponding elements of an elastic line. Except s₃, the momentary shifts _i1 are involved in the expressions (21); the direct dependence of the third harmonic vibration pattern on the first harmonic vibration amplitude corroborates this. As the expressions (21) show, this dependence is cubic.