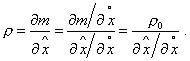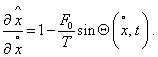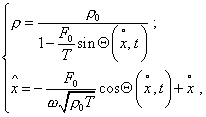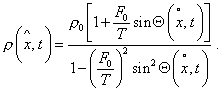rod23

V.2 No 2	23
Compression waves in a rod

To describe the complete pattern of process of a line density time variation, we have to note that the values of density (t) were determined in the excited metric , though in the phase part of (19) is present. To prove it, yield (19) by determining the density directly through the differential on the basis of solution (15), i.e.
	(20)
Provided (17), the expression (15) takes the form
	(21)
whence
	(22)
Substituting (22) into (20), yield an expression fully coinciding with (19). It means that in order to represent the regularity of the line density (, t) we have to take into account the location of point in which this density is observed. Therefore, the resulting regularity (t) is presentable in the parametrical form
	(23)
where the values of non-excited metric are the parameters. The typical form of obtained solutions is presented in Fig. 1. We can see from the construction that with growing amplitude of the external force F₀ the peak in the compression region is sharpen, and the density gradient increases much faster than in the tension region. As (19) shows, at the limiting value F₀ = T, when in the compression region the break forms, in the tension region the density decreases only twice in comparison with ₀ . And at small amplitudes of F₀ the regularity (t) approaches to sinusoidal, one can show this, analysing (19) at F₀ / T <<1.
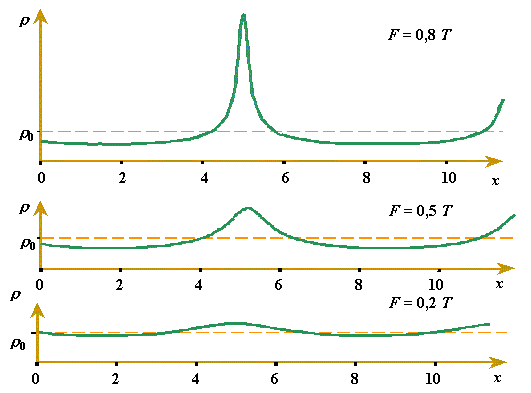
Fig. 1. General form of wave of linear density in semi-infinite thin rod under different amplitudes of external force F₀
To do so, represent (, t) as
	(24)
When the external force amplitude is small, we can neglect the relation F₀ / T squared. Then yield
	(25)
Thus we see in frames of linear modelling an additional band of linear solution, in which the time variation of the thin rod density can be presented as a harmonic function. Just this was identified before with linear vibrations. And the reverse statement follows from this. We see that the non-linear vibrations arise in frames of linear modelling too, its applicability appears wider than in was established before on the basis of harmonic solutions. This enables to refine essentially the lower threshold of non-linear modelling that is based on results obtained by way of linear modelling. Anticipating, we can say that in the light of obtained solutions, in transition of the rod material to the state of fluidity, the value of stiffness T will diminish in the stressed region, and according to (19) the limiting value of F₀ will diminish too. Thus, for real materials we can expect the limiting load diminishing in the compression region on the account of fluidity and due to the growing gradient of density in the compression region that we have revealed in this paper.