СЕЛФ |
4 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
СЕЛФ |
4 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
Пусть имеется две системы отсчёта, в каждой из которых имеются часы одинаковой конструкции, которые можно регулировать. При этом нам неизвестно доподлинно, постоянна ли скорость света при переходе из одной системы отсчёта в другую или нет. Заметим, что данная постановка задачи удовлетворяет как эйнштейновскому релятивизму, так и тем концепциям, которые Вы считаете более совершенными. Нам нужно определить условия синхронизации времени. Описанная модель приведена на рис. 1.
|
|
Рис. 1. Модель синхронизации времени во взаимно движущихся ИСО
|
На представленном рисунке мы
видим штрихованную подвижную систему отсчёта и
нештрихованную неподвижную. Часы обозначены
периодическими структурами. Особенностью данных
структур является то, что импульс посылается из
неподвижной системы в подвижную строго в
определённой точке 1 и принимается тоже в строго
определённой точке 1'. Таким образом, из
неподвижной системы в подвижную идут
синхроимпульсы с некоторой тактовой частотой.
Для синхронизации нас интересуют в первую
очередь трансформации синхроимпульсов при
приёме подвижным наблюдателем. Естественно,
согласно доплеровскому эффекту, в подвижной
системе отсчёта временной интервал несколько
увеличивается, если подвижная система убегает от
неподвижной, и уменьшается, если подвижная
система "догоняет" неподвижную. С одной
стороны, по мнению Эйнштейна, это является
неудобством, поскольку степень растяжения
временных интервалов зависит от взаимного
положения систем отсчёта. Но с другой стороны,
это неоценимое преимущество, поскольку
позволяет наблюдателям получить информацию о
взаимных процессах между этими системами.
Действительно, если наблюдатели однократно
синхронизовали свои часы, то разница в периодах
будет зависеть от времени, которое потребовалось
свету, чтобы пройти путь 1 - 1'. Однако если,
продолжая взаимное движение, наблюдатели
проведут повторные эксперименты, то они увидят,
что временная задержка между тактовыми
импульсами изменилась, - что кстати, полностью
противоречит выводам математического
формализма Эйнштейна, хотя это и есть та самая
реальность, которую Вы предлагаете
рассматривать в начале Вашего письма.
Действительно, если системы отсчёта двигаются
параллельно и их оси х разнесены на величину d,
то при некотором угле
|
|
Рис. 2. Схема расчёта уширения синхроимпульсов
|
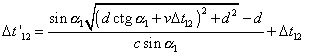 |
(17) |
| и |
 |
(18) |
| где |
| (19) |
| то данная зависимость от угла
|
|
Рис. 3. Графики относительного изменения временного интервала синхроимпульса (сплошные линии) и производной от длительности принимаемого синхроимпульса по мгновенному углу между подвижной и неподвижной системами отсчёта (пунктирные кривые) в зависимости от угла между системами отсчёта и расстояния между ними |
| На рис. 3 мы прежде всего видим,
что при всех расстояниях d кривые
относительного изменения временного интервала
проходят через ноль. Т.е. существует взаимное
положение между системами, когда разность
временных интервалов равна нулю. При малых
расстояниях нулевая точка смещена от положения
вертикали между системами отсчёта, но при
расстояниях порядка 30 световых секунд и более
эта точка строго фиксируется на положении
вертикали между направлениями движения
наблюдателей. В дополнение к этому при большом
расстоянии между системами производная
(обозначенная пунктиром того же цвета, что и сама
кривая) становится строго симметричной
относительно положения вертикали и в этом
положении имеет минимум, совмещённый с
обращением в ноль самой относительной разности
временных интервалов. Заметим также, что кривые
рассчитывались для достаточно большой скорости
движущегося наблюдателя, для которого величина в
30 световых секунд является достаточно малой.
На основе данной зависимости вырисовывается и методика синхронизации. Для её осуществления движущемуся наблюдателю действительно не нужно знать закон трансформации скорости света. Какая бы ни была трансформация этой скорости, минимум производной не изменит своего положения. А в этом минимуме будет соблюдаться РАВЕНСТВО временных интервалов. Для фиксации указанного минимума подвижному наблюдателю достаточно отснять с необходимой точностью закон трансформации временного интервала синхроимпульсов, получаемых от неподвижного наблюдателя, и пересчитать эту зависимость в точку обращения в ноль относительной разности. Поскольку саму относительную разность движущийся наблюдатель экспериментально получить не может, то поиск экстремальной точки он может проводить по изменению производной, взятой от измеряемых экспериментальных данных. Причём при большом расстоянии между системами движущийся наблюдатель может получить эти данные непосредственно, а при малом расстоянии этот наблюдатель может создать зондовую систему отсчёта, послав её с часами-копией на дальнее расстояние от неподвижного наблюдателя. Это позволит уйти от смещения экстремума, наблюдающегося на малых расстояниях между системами отсчёта. Как мы видим, использование
неудобной системы отсчёта как раз и позволяет с
любой заданной экспериментальной точностью
синхронизовать время в системах отсчёта без
каких-либо дополнительных предположений и
трансформаций. При качественно проведенной
синхронизации времени, временные интервалы в
обеих системах отсчёта будут с заданной
экспериментальной точностью одинаковы, и этого
вполне достаточно для относительных
результатов, получаемых на практике. То, что
исследователю придётся достраивать кривые для
получения синхроинтервала, является вполне
нормальной для эксперимента ситуацией. В
качестве примера достаточно привести расчётное
значение абсолютного нуля температуры, который
никто не получил, но его значение в настоящее
время рассчитано с высокой точностью (-273,16о
С). К тому же следует обратить внимание на то, что
в области экстремума кривая производной ведёт
себя очень плавно, что существенно уменьшает
погрешности, связанные с неточностью фиксации
экстремальной точки. Эта особенность и
отражается в том, что звёздное время является
наиболее точным. Как известно, "при наблюдениях на
пассажных инструментах и зенитных трубах
применяется метод регистрации моментов
прохождения звёзд через меридиан. При наблюдении
на призменной астролябии Данжона регистрируются
моменты прохождения звёзд через альмукантарат
(малый круг небесной сферы, параллельный
горизонту) с зенитным расстоянием, равным 30о.
По предварительным данным, погрешности,
характеризующие точность определения времени с
помощью этих инструментов, равны соответственно
19, 18, 16 и 12 мсек" [А.П.
Цитович. Время. ФЭС, т. 1, с. 333]. С учётом
вышеописанной методики синхронизации можно
получить ещё более точное время, синхронизуя его
со среднестатистическими интервалами пульсаций
десятка наиболее стабильных цефеид. Сама
стабильность цефеид будет нам говорить не только
о стабильности процессов в них, но и о том, что мы
находимся по отношению к ним в области
экстремума. Поэтому измеренное подобным образом
время будет наиболее близким к абсолютному по
Ньютону. Из этого напрямую следует, что если два
наблюдателя во взаимно движущихся ИСО будут
синхронизовать свои часы не непосредственно
между собой по Эйнштейну, а в согласии с
ньютоновской механикой с абсолютным временем по
одним и тем же удалённым цефеидам, то с
достаточной экспериментальной точностью оба они
будут иметь общий эталон времени. Имея же эталон
времени, с одновременностью событий уже несложно
определиться. И ещё одно можно отметить в достоинство "неудобной" для релятивистов методики. При снятии кривых изменения временных интервалов, подвижному наблюдателю совсем не обязательно использовать часы, синхронизованные с неподвижным наблюдателем. Для измерения зависимости ему достаточен любой строго периодический процесс в ЕГО собственной системе отсчёта, в единицах которого он может построить зависимость. А построив зависимость, он уже рассчитывает точку экстремума и принимает в качестве эталона то значение его собственных периодических процессов, которое соответствует расчёту. Не удивляемся же мы, когда принимаем за единицу длины 1 650 763,73 периода излучения, соответствующего переходу между уровнями 2р10 и 5d5 атома криптона-86 (ещё и с сотыми долями!). Так и в этом случае. Нюансы же метрологического обеспечения в описанной нами методике могут быть самыми разными. В частности, можно вместо механических маятников применять синхронизацию пачками световых импульсов, генерируемых на установке типа приведенной на рис. 4.
|
|
Рис. 4. Установка для генерации пакетов синхроимпульсов |
На рисунке мы видим, что установка очень напоминает одну из популярных конструкций интерферометра Рождественского, но в отличие от него на вход данной установки подаётся не непрерывное излучение источника, а синхроимпульсы большой скважности. Часть светового пучка сразу отражается полупрозрачным зеркалом на выход прибора, а половина пучка последовательно отражается от внутренних зеркал и тоже попадает на выход несколько сдвинутой во времени по отношению к первой половине пучка. Это и создаёт пакеты парных импульсов, которые могут передаваться неподвижным наблюдателем. Временная задержка легко регулируется расстоянием между внутренними зеркалами и эту регулировку может осуществлять как неподвижный, так и подвижный наблюдатель на своих приборах при корректировке временного интервала. Как мы видим, задача
синхронизации часов хотя и сложна, как и всё в
вопросах метрологических эталонов, но вполне
реализуема. При этом в ИСО все часы
синхронизуются одинаково без каких-либо
трансформаций единицы времени. Достаточно
только, чтобы наблюдатели были действительно
наблюдателями, а не подопытными кроликами
Эйнштейна. Очень сожалею, но это так. С уважением, Сергей и Ольга Каравашкины 18.12.2004 |
Содержание: / 1 / 2 / 3 / 4 /