V.5 No 1 |
S.B. Karavashkin and O.N. Karavashkina | 5 |
| Supplement to the study of classical transverse Doppler effect in respond to received criticism | ||
|
||
V.5 No 1 |
S.B. Karavashkin and O.N. Karavashkina | 5 |
| Supplement to the study of classical transverse Doppler effect in respond to received criticism | ||
|
||
If we solved the problem of longitudinal Doppler effect under condition that the source and receiver move with speeds, correspondingly, v and u as to the stationary frame, general solution will be such as described below. Let in some stationary frame XOY along whose axis x, with positive x, with the speeds v and u, the source A and receiver B move, as it is shown in Fig. 6.
|
Fig. 6
|
Let the source during its motion radiate the array of narrow tact pulses having period TA and we can neglect the duration of these pulses, because of additional systematic error that appears in receiving the pulses of final duration; but we can considerably lessen it, if the receiver detects the heading either back front of the pulse - differentially. Suppose also that the speed of light wave propagation is constant relatively the stationary frame and independent of speeds of source and receiver. Grounding on this statement of problem, suppose that at some instant of time t0 the source and receiver were located at the points xA0 and xB0 as to the stationary frame and at this moment the source has emitted the pulse. If we merely formally approach the calculation of time during which this pulse achieved the receiver, we will yield
|
| (14) |
Going this way, we straight come to your formula (1). But
how much general is this formula? |
| (15) |
is added to above (14). In this light we can mark that the numerator of right-hand part of (14) generally can take both positive and negative values. In particular, this last is possible under condition |
| (16) |
i.e., in case when the initial coordinate of receiver is less than that of radiator. This case is equally real, just as the case |
| (17) |
in which (14) is immediately true. Given the revealed nuance, correct record of (14) will be as follows: |
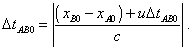 |
(18) |
Consider separately both possible cases that follow from (18). At |
| (19) |
we have |
| (20) |
- just the result which you put into your (1). At |
| (21) |
we have |
| (22) |
which is quite associative, as in this case the observer catches up the source. Noting (20) and (22), we can make more clear the conditions (19) and (21) at which these results were yielded. Substituting (20) into (19), we yield |
| (23) |
If u < c, which is typical for EM waves, (23) takes the shape |
| (24) |
Similarly, substituting (22) into (21), we yield |
| (25) |
| (26) |
As we see, conditions (19) and (21) became much simpler and were reduced to the relation between the initial position of the source and receiver, which is fully consistent with the phenomenology of process. Given this, we can record (18) as |
| (27) |