т.5 No 2 |
1 |
| Дополнение 2. Ответы на вопросы Сергея Хартикова | |
|
|
т.5 No 2 |
1 |
| Дополнение 2. Ответы на вопросы Сергея Хартикова | |
|
|
Дополнение 2. Ответы на вопросы Сергея Хартикова После выхода основной статьи и параллельно с Дополнением 1, нами велась дискуссия с г-ном Хартиковым, на часть вопросов которого мы ответили в первом дополнении. Но у него остались ещё вопросы, хотя, как будет видно из изложения, они существенно трансформировались. Поскольку так или иначе эти вопросы касаются принципиальных аспектов нашей статьи и узловых моментов понимания ошибочности концепции ЧД, мы решили оформить вопросы г-на Хартикова вместе с нашими ответами в Дополнение 2. Для облегчения восприятия, наши предыдущие ответы Хартикову в дискуссии, на которые он опирается, мы обозначим коричнево-зелёным цветом, а вопросы Хартикова сине-зелёным цветом. Цитирование литературы в ответе будет осуществляться стандартным для нашего журнала зелёным цветом. Нумерация вопросов выделена красным. 1. Цитата: “По поводу записи преобразования метрики. Здесь Вы многократно не правы” Сергей, формула (18)
Вашей работы - это вычисление якобиана
преобразования координат в плоском евклидовом
пространстве. В задаче Шварцшильда пространство
изначально риманово, поэтому Ваша формула (18)
заведомо никогда не совпадет с якобианом из
работы Шварцшильда. Формулу (18) Вы вычисляли для
уравнения (16). Посчитайте то же самое для
исходного уравнения (14). И Вы увидите, что
результаты будут отличаться ровно на множитель r2 sin Еще раз повторю
результат, чтобы не было неясностей: корень из
определителя для метрики (14), умноженный на
якобиан r2
sin Мы начнём наш ответ с опровержения Вашего утверждения, что мы якобы определяли якобиан в плоском евклидовом пространстве, а Шварцшильд в римановом. При переходе от метрики в прямоугольных координатах (выражение (14) нашей статьи) |
| (1) |
к метрике в сферических координатах (выражение (16) нашей статьи) |
| (2) |
Шварцшильд воспользовался стандартными формулами преобразования именно для плоского евклидового пространства (выражение (15) нашей статьи) |
| (3) |
которое Вы безусловно не могли не заметить, акцентируя своё внимание на предыдущей и последующей формулах. В римановом пространстве преобразование (3) в общем случае не справедливо. В предшествующем ответе, кроме указанной Вами цитаты, мы ещё очень и очень много написали, и в частности по данному конкретному поводу: “Правильно в Вашем понимании будет записывать |
| (4) |
разделяя метрический тензор и коэффициент Fik , хотя и в этом случае оказывается тоже необходимо учитывать G и H. :-)” После этого мы обосновали необходимость учёта при преобразованиях указанных коэффициентов. В свете этого интересно напомнить претензию, которую мы выдвигали к преобразованию (1) в (2) в нашей статье. “Согласно существующему математическому формализму тензорного анализа, в данном случае ортогональной метрики |
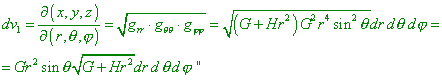 |
(5) |
[1, с. 6]. Как мы видим, в выражении (5) стоит якобиан в самом общем виде, который и используется при преобразованиях в криволинейных координатах. И именно на основании выражения (5) мы сделали заключение о неправильности мнения Шварцшильда, которое заключалось в следующем: “При этом элемент объема в сферических координатах равен |
| (6) |
так что якобиан
преобразования от старых координат к новым, равный r2 sin |
| (7) |
Шварцшильд уже не мог удовлетворить равенству |
| (8) |
поскольку он должен был удовлетворить иному равенству |
| (9) |
[1, с. 6]. Так что Ваши претензии к
тексту нашей статьи в данном случае полностью
необоснованны. Как раз не мы, а Шварцшильд
преобразовывал в метрике евклидового
пространства. Аналогично, описание
проделанных Вами расчётов, о которых Вы пишете,
не отвечает математическим операциям, которые
должны в реальности выполняться при переходе от
(1) к (2) с последующим переходом (9). Вопрос ведь не в
том, что “корень из определителя для
метрики (1), умноженный на якобиан r2 sin |
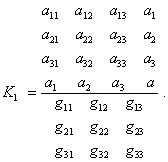 |
(10) |
В этот инвариант должны войти
как раз те коэффициенты H и G, наличие
которых в наших выкладках Вы посчитали
неправомерным. |