СЕЛФ |
16 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
СЕЛФ |
16 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
|
Методика поиска решения некоторых типов нелинейного волнового уравнения С.Б. Каравашкин, О.Н. КаравашкинаУкраина, 61140, Харьков, проспект Гагарина, 38, кв.187 Тел.: (057) 7370624 e-mail: selftrans@yandex.ru , selflab@mail.ru Приведена методика поиска решения нелинейных волновых уравнений типа u’’ + g(t)u = 0 и u’’ + g(u)u = 0, а также рассмотрена перспектива расширения области применения методики на другие типы нелинейных волновых уравнений. Ключевые слова: волновая физика, математическая физика, нелинейные дифференциальные уравнения второго порядка, волновое уравнение 1. Введение Как известно, волновое уравнение играет важную роль в моделировании физических процессов во многих задачах термодинамики, механики, теории поля и т.д. Причём во многих случаях мы при моделировании сталкиваемся с нелинейными типами волнового уравнения и при отсутствии подходов к их решению вынуждены или неоправданно линеаризовать задачу, или ограничиваться численными методами решения, что существенно ограничивает возможности дальнейшего развития решений в приложениях и делает невозможным полный анализ модели. В данной работе мы представим методику решения нелинейных уравнений двух типов, важных для задач моделирования, и покажем некоторые перспективы расширения её применения на другие типы нелинейного волнового уравнения. 2. Методика нахождения решения волнового уравнения типа u’’ + g(t)u = 0 Как уже определено в названии данного раздела, рассмотрим волновое уравнение типа |
| (1) |
Чтобы определиться с направлением поиска, сначала проведем некоторые преобразования в левой части. Для этого умножим второе слагаемое на - i2, прибавим и вычтем выражение if (t) du/dt , где f (t) - некоторая вспомогательная, дифференцируемая на интервале функция времени, а также разобьем функцию g (t) на два аддитивных слагаемых |
| (2) |
где k (t) некоторая вспомогательная, дифференцируемая на интервале функция времени. После группировки получим |
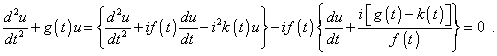 |
(3) |
Для нахождения решения уравнения (3) необходимо, чтобы выражения в фигурных скобках были идентичными. Чтобы добиться этого, мы можем воспользоваться известным выражением, вытекающим из законов дифференцирования |
| (4) |
Сравнивая (4) с первой фигурной скобкой в (3), получим |
| (5) |
откуда следует |
| (6) |
На основании (4)- (6) мы можем сделать вывод, что выражения в фигурных скобках в (3) будут тождественно равны в случае, если |
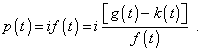 |
(7) |
Из (7) с учетом (6) следует |
| (8) |
или |
| (9) |
Полученное нами выражение (9) определяет неизвестную нам функцию f (t) , найдя которую, мы получим решение общего уравнения (1). Решение дифференциального уравнения (9) удобно искать в виде гармонического ряда по аналогии с методикой, изложенной в нашей работе [1]. Для этого необходимо представить функцию g (t) также в виде гармонического ряда |
| (10) |
где gm являются некоторыми постоянными Фурье-разложения. Причем в общем случае они могут быть и комплексными величинами. С учетом (10) мы будем искать решение уравнения (9) также в виде гармонического ряда |
| (11) |
Производя дифференцирование (11) по времени и подставляя результат в (9) совместно с (10) и (11), получим |
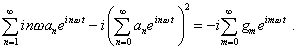 |
(12) |
Из выражения (12) мы видим, что комплексная единица может быть сокращена в правой и левой частях и при действительных коэффициентах gm уравнение становится тоже действительным. Идя далее, мы можем представить (12) в виде системы алгебраических уравнений, приравнивая коэффициенты при соответствующих экспонентах правой и левой части. Запишем первые из этих уравнений. m = 0 |
| (13) |
откуда |
| (14) |
m = 1 |
| (15) |
откуда |
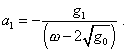 |
(16) |
m = 2 |
| (17) |
откуда |
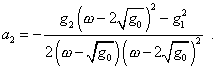 |
(18) |
m = 3 |
| (19) |
откуда |
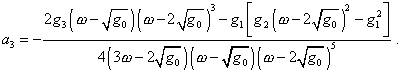 |
(20) |
Как следует из анализа первых
четырех членов, система является рекуррентной и
мы можем последовательно определять все
коэффициенты разложения через предыдущие. Кроме
того, из полученных решений видно, что полученный
ряд быстро убывающий, пропорционально 1/ Определив вид функции f (t) и тем самым выяснив, что определяющее выражение (9) имеет решение, мы можем вернуться к выражению (3) и записать его в виде |
| (21) |
где |
| (22) |
Из (21), (22) мы видим, что принимая |
| (23) |
мы тем самым обращаем в ноль и уравнение (21). Следовательно, условие (23) является уравнением, определяющим одно из частных решений уравнения (21), а значит, и исходного уравнения (1). Решение же для (23) очевидно: |
| (24) |
где C1 - некоторая постоянная, определяемая условиями задачи. Учитывая в дополнение к этому определённые нами коэффициенты ряда (11), мы можем проинтегрировать f (t) по времени и подставить в правую часть (24). При этом получим |
| (25) |
Чтобы определить второе частное решение исходного волнового уравнения (1), достаточно несколько иначе перегруппировать члены в выражении (3), записав это выражение в виде |
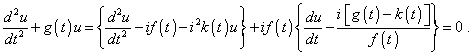 |
(26) |
Проходя далее весь вышеописанный путь, получим |
| (27) |
где C2 также является постоянной, определяемой условиями задачи. Объединяя (25) и (27), получим окончательно |
| (28) |
Это и есть искомое нами решение волнового уравнения (1). В частном случае |
| (29) |
все коэффициенты разложения (10), кроме нулевого, обращаются в ноль и решение (28) принимает стандартный вид |
| (30) |
что подтверждает правильность сделанных нами преобразований. |
Содержание: / 16 / 17 /