т.6 No 1 |
С.Б. Каравашкин и О.Н. Каравашкина |
1 |
| Дополнение 1: О функции Грина | ||
|
||
т.6 No 1 |
С.Б. Каравашкин и О.Н. Каравашкина |
1 |
| Дополнение 1: О функции Грина | ||
|
||
Дополнение 1: О функции Грина От: tadchem Дата: Пн 13 Марта 2006 00:14 Е-почта: "tadchem" <thomas.david...@dla.mil> Группы: sci.physics, alt.sci.physics, alt.sci.physics.new-theories, alt.astronomy, sci.physics.relativity Was there something about the chapter on Greens Functions that you missed? http://www.math.lsa.umich.edu/~vbooth/gf.pdf Tom Davidson Richmond, VA Перевод: Имеет ли это отношение к главе по функции Грина, которую Вы пропустили? Предварительный ответ Уважаемый Том, прежде всего, огромное спасибо за статью. Прекрасное изложение и строгие формулировки. Именно они показывают отличие описанного нами подхода от того, который предпринимается при решении задачи с помощью функции Грина. Мы опустили эту часть, поскольку не хотели вдаваться в дополнительные объяснения, почему решения с помощью функции Грина, в действительности являются ошибочными. Да-да, я не оговорился, но прошу понять то, что я скажу далее. Для простоты возьмём первую задачу, представленную на Вашем сайте. Как известно, “функция Грина имеет простой физический смысл. Это решение задачи для единичного источника |
(в символах Вашего сайта) [М.Л. Краснов. Интегральные уравнения]. При этом функция Грина G (x, x0) будет удовлетворять решению в том случае, если |
| (1) |
где Lx – оператор однородного дифференциального уравнения, соответствующего заданному неоднородному. Вот оно, уравнение, которому в действительности должна удовлетворять функция Грина. А что делают? И на Вашем сайте, и обычно ищут решение уравнения |
| (2) |
справа и слева от точки x0, а затем сшивают решения на основе искусственного условия непрерывности функции в самой точке. Исходя из этого и у Вас была решена система уравнений. Но решение (2) не соответствует (1) именно в точке x0. В этой точке уравнение (1) становится неоднородным! Но функция Грина, найденная существующими методами сшивки, не способна учесть эту принципиально важную особенность. И в этом очень легко убедиться. Возьмите любую определённую подобным образом функцию Грина и подставьте в (1) при условии x = x0. Вы получите равенство нулю во всем интервале, включая и точку x0, а не дельта-функцию. Но это не решение, поскольку при этом воздействие на решение оператором дифференциального уравнения L обратит функцию Грина в ноль, а должно дать дельта-функцию, чтобы, умножив ее на функцию правой части уравнения и проинтегрировав, получить правую часть исходного дифференциального уравнения. Таким образом только кажется, что ищется решение неоднородного дифференциального уравнения. В действительности находят некоторую форму решения однородного уравнения. ;-) Поэтому решения, которые будут получаться нашей методикой, будут в общем случае отличаться от численных решений, полученных с помощью функции Грина. Из наших материалов можно легко видеть, что у нас описанной проблемы нет и мы получаем аналитические решения без дельта-функции, причём в ряде случаев получаем решения даже не в виде Фурье-разложения, но в аналитическом виде, что в случае функции Грина принципиально невозможно. Последнее, кстати, показано в статье. Но, возможно, Вы правы в том, что написанное Вам нужно было бы оформить более подробно и в соответствующих развёрнутых доказательствах. Мы это сделаем и известим Вас о дополнении к статье. Надеюсь на внимательный Ваш анализ сказанного мной, поскольку сам понимаю, насколько это неожиданно и непривычно Вам. Сергей Полный ответ Как я и обещал, в полном ответе я попробую обосновать строго утверждение о некорректности решения задачи с использованием функции Грина. Для этого прежде всего запишем стандартные требования, которые предъявляются к данной функции при поиске решения стандартного дифференциального уравнения второй степени, типа |
| (1) |
с краевыми условиями |
| (2) |
“Определение:
Функцией Грина G (t, s) краевой
задачи (1)- (2) называется функция двух переменных,
определённых в квадрате a 1) Lt G (t, s) = 0 при t < s и t > s, т.к. G (t, s) как функция t удовлетворяет при указанных значениях t и s уравнению (1); 2) Функция G (t, s) удовлетворяет поставленным граничным условиям |
| (3) |
3) G (t, s) непрерывна при t = s: |
| (4) |
4) Производная |
| (5) |
[1, с. 221]. Данные условия должны обеспечить выполнение равенства |
| (6) |
“Поэтому условия 1) и 4) можно заменить условием |
| (7) |
[1, с. 222]. Это модифицированное условие (7) обусловлено тем, что “решение краевой задачи (1) - (2) дается формулой |
| (8) |
[1, с. 222]. При этом для выражения (8) должна выполняться цепочка равенств |
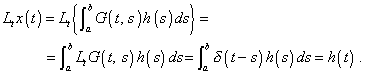 |
(9) |
Мы видим прямое использование в (9) выражения (7). Причем, чтобы (9) строго выполнялось, необходимо, чтобы и (7) выполнялось строго. Теперь с этой точки зрения проанализируем методику нахождения функции Грина, которая практикуется в настоящее время и представлена, в том числе, и на указанном Вами сайте. Рассмотрим это на конкретном примере, изложенном в упоминавшейся выше работе Краснова [1], хотя у него приведена стандартная методика, с точностью до незначительных нюансов, практикуемая и другими исследователями. Рассмотрим уравнение типа (1) |
| (10) |
| (11) |
“Построим функцию Грина задачи (10)- (11). Общее решение однородного уравнения |
| (12) |
соответствующего уравнению (10), имеет вид |
| (13) |
[1, с. 222]. Но какое отношение имеет (12) к
уравнению (7), которому в действительности должна
строго удовлетворять функция Грина? Только то,
что вне точки t = s функция |
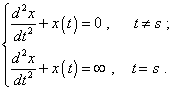 |
(14) |
При этом решение второго уравнения откровенно не может быть получено ни в явном виде, ни в виде рядов. Если же мы исключаем точку t = s из рассмотрения, то тем самым мы исключаем и дельта-функцию из правой части уравнения и сразу признаём, что искомое решение таковым не является, поскольку при этом цепочка равенств (9) даст не правую часть исходного дифференциального уравнения, а ноль. И это легко показать, продолжив анализ построения функции Грина. “Поскольку функция G (t, s) должна быть решением этого однородного уравнения при t < s и при t > s, представим её в виде |
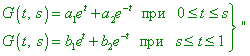 |
(15) |
[1, с. 223]. Обратим внимание на границы интервалов в выражении (15). В посылке фигурируют строгие неравенства, в то время как в (15) эти строгие неравенства заменены на нестрогие. Но что это означает? Это означает то, что математики прекрасно себе представляли, когда переписывали из книги в книгу, что уравнением (12) не охватывается принципиально важная точка t = s. Также они прекрасно понимали, что (15) должна была бы содержать три уравнения, и третье должно было бы описывать именно решение в указанной точке, которое, как мы показали выше, получено быть не может. Именно поэтому была произведена молчаливая подмена символов, которая, в сущности, разрушила всё построение функции Грина как решения дифференциального уравнения (10). Ведь и первое, и второе решение в (15) удовлетворяет однородному уравнению (12), а значит, и в точке t = s функция Грина тоже будет удовлетворять этому уравнению, а не второму уравнению системы (14), со всеми последствиями для базового доказательства, определённого цепочкой равенств (9). Кстати, если подходить строго к данному моменту построения функции Грина, то изменение пути построения с дифференциальной формы, как это описано выше, к интегральной, как представлено на указанном Вами сайте, ничего принципиально не меняет, поскольку вместо выражения |
| (16) |
должно было бы фигурировать выражение |
| (17) |
в котором средний интеграл Вы никогда не сможете определить ни прямо, ни численно, так как в этом интеграле функция Грина должна быть решением именно второго уравнения системы (14). Без этого Ваша функция Грина не удовлетворяет четвертому условию определения данной функции, как и рассматриваемая выше функция (15). В последнем случае это очень просто прямо показать, поскольку цитируемый автор довёл построение до конца и представил эту функцию в окончательном виде: |
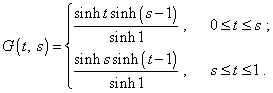 |
(18) |
Как мы видим из (18), конечная система также состоит из двух решений и контролируемая нами точка t = s включается в область определения данных решений. Первая производная от (18) по времени будет иметь вид |
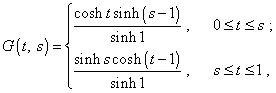 |
(19) |
и вторая производная соответственно будет повторять (18). А следовательно, во всём интервале определения решение будет удовлетворять соответствующему однородному дифференциальному уравнению (12), но не тому дифференциальному уравнению (7), которое и определяет соответствие функции Грина исходному дифференциальному уравнению. Если же говорить, чему удовлетворяет решение, полученное на основе подобной подмены неоднородного уравнения с дельта-функцией в правой части однородным уравнением, то заключение об этом вытекает из самого способа построения функции Грина. Выше мы показали, что при воздействии оператора на интегральную форму решения с функцией Грина, удовлетворяющей однородному уравнению, вместо правой части мы получаем ноль. А значит, решение в интегральной форме, построенное на основе функции Грина, удовлетворяет линейному однородному уравнению, поскольку, как правило, в левой части обычно ставится именно линейное уравнение, решения которого известны. В нашем же подходе, описанном в статье, всех вышеуказанных проблем нет, поскольку мы вообще не используем разрывных функций, а находим решение стандартными методами теории дифференциальных уравнений, чем с принципе и отличается наш метод от метода, основанного на построении функции Грина. Литература: 1. Краснов М.Л. Интегральные уравнения. Москва, Наука, 1975, 303 с. |