|
т.7 No
1 |
1 |
| Диалог о
сохранении энергии и импульса |

|
Диалог о
сохранении энергии и импульса
ВЛАДИМИР: Что-то я забуксовал, уважаемый Сергей, на стр. 73 Вашей
работы “Проблемы физического времени в
современной физике”. Не
совсем понятно, о каком сохранении импульса и
энергии Вы ведете речь для случая покоящейся
системы S? Ведь система частичек во внешнем
поле не замкнута и они движутся с ускорением?
Непонятно.
СЕРГЕЙ: Как мы показали с точки
зрения классической механики, в однородном поле
законы сохранения “переходят” из
неинерциальной системы отсчета в инерциальную
за счет того, что ускорение самой системы отсчета
идентично ускорению материальных тел.
ВЛАДИМИР: Я хотел обратить Ваше
внимание, что сам оборот речи (цитирую)
"Таким образом, если в одной
системе отсчета действует закон сохранения
импульса |
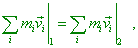 |
(6.38)(d1.1) |
где 1 и 2 обозначают
сумму импульсов до и после некоторого процесса,
происходящего в данной системе, то и в другой
системе отсчета в соответствии с (6.36) будет
выполняться равенство" не должен иметь
место в классической физике, поскольку все
законы сохранения она формулирует для одной
(неподвижной) ИСО. Дальше, если угодно
рассмотреть ту же систему из другой ИСО, то не
останутся прежними ни импульс ни кинетическая
энергия системы, а наоборот, они изменятся и
классическая физика указывает, каким образом они
изменятся.
СЕРГЕЙ: Вы правильно пишете,
уважаемый Владимир, а скажите мне пожалуйста,
если в одной инерциальной системе отсчета законы
сохранения энергии и импульса сохраняются, они в
другой системе отсчета сохраняются? С точки
зрения классической физики, конечно. 
ВЛАДИМИР: С точки зрения
классической физики во всех ИСО законы
сохранения энергии и импульса работают, конечно,
но энергия с импульсом не сохраняются при
переходе из одной ИСО в другую.
СЕРГЕЙ: Численные значения
энергии и импульса системы, естественно, при
преобразованиях из одной СО в другую изменяются.
И могу Вам заметить, что и релятивисты будут
согласны с фактом этих изменений. Но ведь законы
сохранения записываются не для переходов между
СО, а в качестве сохранения импульса ли, энергии
ли при каких-либо взаимодействиях внутри
материальной системы тел в данной СО. Не так ли?
Так вот я Вам и задал вопрос: в одной системе
закон сохранения при некотором взаимодействии
внутри системы материальных тел соблюдается.
Будет ли этот закон соблюдаться при наблюдении
этого взаимодействия из другой, движущейся
инерциально, системы отсчета? Не это ли и
определяет то, что Вы вкладываете в понятие
“законы сохранения энергии и импульса
работают”? 
ВЛАДИМИР: С точки зрения
классической физики законы сохранения для
замкнутых систем должны соблюдаться при
наблюдении системы из любой ИСО. Для разных ИСО
добавляется разная константа, ответственная за
движение центра масс системы.
СЕРГЕЙ: Конечно, константы
разные. И у релятивистов меры разнятся. Но ведь
если законы сохранения переходят из одной
системы отсчета в другую, то мы это наблюдаем так,
как показано в формулах (6.34)–(6.45). То есть, имеем
равенство – например, суммы импульсов до
взаимодействия и суммы импульсов после
взаимодействия. Перешли из одной системы в
другую и получаем равенство тех же сумм, но уже с
другими значениями скоростей, которые
соответствуют другой СО. Константы же могут
фигурировать только тогда, когда мы
рассматриваем саму сумму импульсов системы или
полную энергию системы. Когда же мы приравниваем
одно другому, константы уходят, не так ли?
ВЛАДИМИР: Тогда, с Вашего
позволения, вернемся к постановке задачи.
Дана некоторая область
пространства, на которую воздействует
однородное гравитационное поле и есть две
системы отсчета: S – инерциальная
(неподвижная) система отсчета и свободно
падающая система отсчета S', а также дана
некоторая компактная совокупность n масс mi ,
i = 1, 2, 3, ... , n, каждая из которых в
начальный момент t0 обладает
скоростью v'i относительно свободно
падающей системы отсчета S'. Я так понимаю,
что и относительно системы отсчета S в
начальный момент времени скорости те же.
Рассмотрение ведем в рамках
классической физики.
Формулы (6.34)–(6.37) верны.
Следующее затем утверждение: "Таким образом, если в одной
системе отсчета действует закон сохранения
импульса (6.38), где 1 и 2 обозначают сумму импульсов
до и после некоторого процесса, происходящего в
данной системе, то и в другой системе отсчета в
соответствии с (6.36) будет выполняться
равенство" – неверно.
И я уже писал об этом. Почему? Потому что в
сопутствующей системе S' на все n масс mi никакая сила не действует
(равнодействующая силы тяжести и силы инерции
равна нулю). А в системе отсчета S на все массы
действует неуравновешенная сила тяжести.
Поэтому системы отсчета принципиально
отличаются друг от друга. В одной из них, S',
совокупность масс может рассматриваться как
замкнутая система, и в ней будут действовать
законы сохранения импульса и энергии системы. А в
другой, S, та же совокупность масс не может
рассматриваться как замкнутая система и в ней
законы сохранения выполняться не будут.
И формула (6.36) тут ни при чем.
Вернее, именно формула (6.36) говорит о том, что если
есть (6.39), то никак не может быть (6.38). Ведь ясно,
что если момент времени “1” это начальный t0
и в этот момент v и v’ совпадали, то в
момент времени “2” к “законным” приращениям v’
(в системе S' ) в системе S добавилась
систематическая vrel . Таким образом,
утверждаемого Вами соотношения (6.38) нет и не
должно быть.
СЕРГЕЙ: В этом-то и фокус,
уважаемый Владимир! После выражения (6.39) есть
вывод, который как раз и показывает, как именно
расслаивается исходная сумма на две
составляющие. Если при этом в каждом из выражений
вторая сумма не будет зависеть от процессов,
происходящих внутри системы материальных тел
(т.е. не будет содержать параметров, связанных со
скоростями этих тел и их местоположением в
пространстве), то при подстановке указанных
выражений в (6.38), вторые суммы сократятся и
останутся только члены, содержащие параметры в
штрихованной системе отсчета, и равенство
приобретет тот же самый вид, но в других
параметрах. В классическом формализме это имеет
место при переходе между инерциальными
системами отсчета (вследствие чего и говорят об
эквивалентности инерциальных систем
относительно законов динамики) и при переходе
между инерциальными системами и системами
отсчета, свободно падающими в однородном поле
тяжести, что попытался в своих целях
использовать Эйнштейн. Только в этих двух
случаях вторые суммы не будут содержать
скоростей и координат систем отсчета. Вне этого
эквивалентность нарушается.
ВЛАДИМИР: С тем, что “тот же
вид”, я согласен. Ведь выражение для
кинетической энергии не меняет своего вида
при переходе между системами. Но вывод после
выражения (6.39) полностью неправильный, и вот
почему.
Вы утверждаете:
“Пусть в неподвижной системе отсчета
выполняется закон сохранения энергии, при этом
мы можем записать (6.42)”, из чего следует, что
левые части (6.43) и (6.44) равны.
Во-первых, само утверждение,
начинающееся словом “пусть
...” выглядит заранее неверным или
невыполнимым, поскольку приращение кинетической
энергии частиц, возникающее вследствие разгона в
поле тяжести, не может быть ничем
скомпенсировано внутри замкнутой системы самих
частиц.
Но даже если мы закроем глаза на
неправильность исходного положения, то все равно
далее мы неизбежно придем к:
“Теперь, чтобы получить из (6.43)
и (6.44) уравнение сохранения энергии для
движущейся системы отсчета, достаточно учесть,
что вторые слагаемые в правых частях обоих
выражений равны”
Так вот, не равны, уважаемый
Сергей. Каждое составляющее суммы (вторые
слагаемые в правых частях) в случае “2” больше
соответствующего слагаемого в сумме “1” на
величину g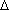 t, где t, где 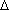 t есть разность между
моментами времени. Посмотрите еще раз
внимательно. Откажитесь в конце концов от
принятой Вами системы обозначений случаев как
“1” и “2”, которое не позволяет детально
рассмотреть выражения, и Вы увидите, что
приравниваете неравные величины. Соответственно
и утверждение “а третьи слагаемые
равны из условия сохранения импульса системы”
неверно, поскольку импульс сохраняется только
относительно системы S’ , но не относительно
системы S . t есть разность между
моментами времени. Посмотрите еще раз
внимательно. Откажитесь в конце концов от
принятой Вами системы обозначений случаев как
“1” и “2”, которое не позволяет детально
рассмотреть выражения, и Вы увидите, что
приравниваете неравные величины. Соответственно
и утверждение “а третьи слагаемые
равны из условия сохранения импульса системы”
неверно, поскольку импульс сохраняется только
относительно системы S’ , но не относительно
системы S .
Кстати, я согласен с (6.45). Это
выражение верно в силу законов сохранения в
замкнутой системе отсчета. Но зачем было идти к
верному (6.45) через неверные (6.42)–(6.45) – не понимаю.
СЕРГЕЙ:
1.Давайте, уважаемый Владимир,
не торопиться по пути поиска неправильного.
Бывает же и так, что за неправильное принимается
непонятое. Не так ли? Вот, к примеру, Вы выше тоже
утверждали, что переход от уравнения (6.38) к
уравнению (6.39) некорректен. Сейчас Вы
согласились, что в законе сохранения импульсов в
каждой системе отсчета закон сохранения должен
иметь один и тот же вид. При этом Вы не сняли
вопрос о переходе от одной системы отсчета в
другую в законе сохранения импульса, перескочив
на закон сохранения энергии.
2.Вместе с тем, чтобы для одного
и того же взаимодействия законы сохранения в
разных системах отсчета имели тот же самый вид,
все лишние зависимости должны как-то из этих
законов исчезать (или появляться), сохраняя
законы неизменными. Не так ли? 
3.Давайте все же закончим с
поднятым Вами вопросом и выясним, правомерен ли
переход из одной системы отсчета в другую с
помощью уравнений, приведенных в обоснование
(6.39).
Для этого я предлагаю вернуться
к конкретной схеме, которая была в первом
варианте работы и в которой Вы меня справедливо
поправили. Разобрав эту схему, мы как раз и
уясним, что и как конкретно переходит. Вы не
против?
ВЛАДИМИР:
1.Видите ли, уважаемый Сергей, я
и не спорил о виде законов сохранения,
поэтому и согласился. Но вид законов – это одно, а
выполнение – другое.
2.Нет, не так. Вид закона – это,
например, сумма импульсов равна const. “Лишние”
зависимости в разных системах отсчета должны
давать тоже const, а не “уничтожаться”. Тогда
законы верны или неизменны, как Вы выражаетесь.
Но нельзя забывать, что законы сохранения
“автоматически” действуют или верны только для
замкнутых систем. А у Вас система частиц
находится во внешнем поле, т.е. именно не
замкнута. Поэтому я считаю, что все выкладки
(6.38)–(6.44) необходимо пересмотреть.
3.Я не против любой формы
рассмотрения, если Вы считаете что это облегчит
путь к истине. |
|
СЕРГЕЙ: Здесь мы, уважаемый
Владимир, подходим к первому очень интересному
моменту нашей дискуссии. Из Вашего второго
пункта следует: “законы сохранения
“автоматически” действуют или верны только для
замкнутых систем”. И это подтверждает внешне
существующие определения законов сохранения:
“Сохранения законы
– физические закономерности, согласно которым
численные значения некоторых физических величин
не изменяются с течением времени в любых
физических процессах (иногда в определенном
классе процессов)” [М.Б. Менский. Сохранения
законы. Физический энциклопедический словарь,
т. 4, с. 591, М., Советская энциклопедия, 1965].
Как мы видим, в определении
также указано сохранение численной величины во
времени, что предполагает консервативность
системы материальных тел.
Вместе с этим данное
определение, как и Ваше утверждение,
предполагает, что если система материальных тел
открыта, т.е. не консервативна, и находится,
например, в поле внешних сил, то в этой системе
законы сохранения не выполняются? Прекрасно. А
теперь, с Вашего позволения, мы перейдем к нашей
старой задаче, которую договорились
рассмотреть.
Думаю, Вы узнаете построения на
рис. 1, на котором представлена модель
взаимодействия некоторого тела с массивной
стенкой, находящихся во внешнем поле
гравитирующего тела. Как
Вы помните, условие задачи и начало расчета имели
следующий вид.
Пусть имеется некоторый
гравитирующий центр и в нем находятся две
системы отсчета, одна из которых (нештрихованная)
инерциальна и неподвижна относительно
гравитирующего тела, а вторая (штрихованная)
свободно падает в поле гравитирующего тела.
Пусть также в некоторый начальный момент времени
данные системы совмещены и начальная скорость
свободно падающей системы отсчета в этот момент
равна нулю. Наконец, пусть в свободно падающей
системе отсчета находится некоторое тело массой m
и массивная стенка, расположенная в начальный
момент времени на расстоянии L' вдоль
направления к гравитирующему центру, как
показано на рис. 1.
|

Рис. 1. Схема для расчета
движения материального тела, взаимодействующего
с упругой преградой в свободно падающей
(штрихованной) системе отсчета
|
Пусть в начальный момент
времени материальному телу придается некоторая
скорость v'0 относительно свободно
падающей системы отсчета в направлении к стенке.
Рассмотрим, на какое расстояние отскочит
исследуемое тело (при условии полностью упругого
отражения) в свободно падающей системе отсчета
за время, равное затраченному на его полет к
стенке. Ведь если говорить об эквивалентности
законов в инерциальных и неинерциальных
системах отсчета, то в первую очередь необходимо
убедиться, что при нерелятивистских скоростях в
обеих системах одинаково выполняются законы
сохранения импульса и энергии. Этому, по сути, и
посвящен нижеследующий расчет.
Расчет будем вести в
инерциальной системе отсчета, причем будем
одновременно прослеживать траекторию
исследуемого тела и точки A' свободно
падающей системы отсчета, из которой исследуемое
тело начало свое движение, чтобы в конце сравнить
положение тела и положение указанной исходной
точки.
Начнем с траектории
материального тела. Поскольку оно обладает
массой, то его движение по отношению к
инерциальной системе отсчета будет
равноускоренным, а следовательно, равномерным по
отношению к свободно падающей системе отсчета.
На первом участке траектории, т.е. при движении к
стенке, уравнения движения с точки зрения
инерциальной системы отсчета будут иметь вид |
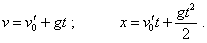 |
(d1.2) |
Тело достигнет стенки в момент
времени |
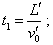 |
(d1.3) |
при этом его скорость с точки
зрения свободно падающей системы отсчета будет
оставаться равной начальной, т.е.v'1
= v'0 , но с точки зрения неподвижной
системы отсчета скорость тела с учетом (d1.2) и (d1.3)
будет равна |
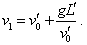 |
(d1.4) |
Это событие произойдет в точке x'1
= L' свободно падающей системы отсчета и в соответствующей ей точке |
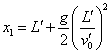 |
(d1.5) |
инерциальной системы отсчета.
Параллельно с телом в инерциальной системе
отсчета будет смещаться и исходная точка A' .
В момент t1 она вместе с началом координат
свободно падающей системы отсчета будет
занимать положение |
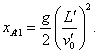 |
(d1.6) |
Теперь по ходу задачи нам нужно
рассчитать процесс отражения исследуемого нами
тела от массивной стенки с точки зрения
неподвижной системы отсчета. Какие законы нам
нужно при этом использовать, если стенка и тело
движутся равноускоренно во внешнем
гравитационном поле и эта система материальных
тел с точки зрения неподвижной системы отсчета
является открытой?
ВЛАДИМИР: Для расчета “с точки зрения
неподвижной системы отсчета” нужно использовать законы сохранения при
упругом ударе двух тел, рассматривая его (удар)
как процесс без длительности во времени.
СЕРГЕЙ: Отлично, уважаемый
Владимир. Но как же в таком случае быть с
общепринятым утверждением, что “Сохранения
законы – физические закономерности, согласно
которым численные значения некоторых физических
величин не изменяются с течением времени”?
Не следует ли из этого, что существующая
трактовка не охватывает всего комплекса законов?
Ведь если существуют законы сохранения, которые
мы можем применять к процессам “без
длительности во времени”, то эти законы и по
определению, и по записи должны отличаться от
законов сохранения, определяющих
консервативность системы материальных тел,
определяемых во времени, не так ли?
ВЛАДИМИР: Совершенно верно,
уважаемый Сергей. Но в приведенной Вами
формулировке речь идет о сохранении значений
“некоторых физических величин”
рассматриваемой физической системы в течение
времени, и здесь именно важна замкнутость
системы, а взаимодействия – это отдельная песня.
Они не однозначны по отношению к законам
сохранения. При разных взаимодействиях законы
сохранения могут работать не все. Тот же
неупругий удар – закон сохранения импульса
работает, а закон сохранения энергии – нет. В
модели упругого удара предполагается отсутствие
потерь механической энергии, поэтому работают и
закон сохранения импульса, и закон сохранения
энергии.
Я хочу сказать, что каждый вид
взаимодействия в смысле законов сохранения
рассматривается отдельно. И параметр “время”
при этом не всегда учитывается. В частности, в
модели удара им пренебрегают. Рассматривают
баланс мгновенных значений импульсов и энергий
“до” и “после”.
СЕРГЕЙ: И именно в таком смысле
баланса мгновенных значений импульсов и энергий
“до” и “после” записаны выражения сохранения
импульса и энергии при взаимодействии внутри
системы n тел, которые у Вас вызвали
возражения.
С другой стороны, обратите
пожалуйста внимание на тот факт, что говоря о
нарушении законов сохранения, Вы говорите о
нелинейных процессах – таких, как неупругий
удар, – при которых и в рамках одной инерциальной
системы отсчета закон сохранения импульса тоже
не выполняется и требуется вводить
дополнительные согласующие коэффициенты,
определяемые, как правило, экспериментально и с
достаточно существенной величиной погрешности,
когда сложно определить справедливость той или
иной идеальной концепции, тем более, когда эти
конкурирующие концепции дают близкие значения в
области достижимых нами скоростей и ускорений. В
рамках же идеально упругих тел, материальных
точек, идеальных связей, т.е. тех идеализаций,
которыми оперирует классическая теоретическая
механика, можно с уверенностью говорить, что в
однородном гравитационном поле в свободно
падающей системе отсчета сохраняются и законы
консервативности, т.е. законы сохранения энергии
и импульса движения материальной точки во
времени, и законы сохранения энергии и импульса
при идеальном взаимодействии тел.
Другое дело, что связь между
инерциальными и неинерциальными системами
отсчета не сохраняет, например, условие
консервативности, поскольку в гравитационном
поле в инерциальной системе отсчета суммарный
импульс и суммарная энергия будут постоянно
изменяться, а в свободно падающей системе
отсчета эти параметры будут оставаться
постоянными.
Но для релятивистов ведь не
важно, что не будут сохраняться параметры при
переходе между инерциальными и неинерциальными
системами отсчета. Смотрите, как они пишут: “Наличие
гравитационного поля вызывает такие явления в
инерциальных системах отсчета, которые локально
неотличимы от инерциального ускорения, которое
можно было бы наблюдать в неинерциальной системе
отсчета” [П. Бергман. Загадка
гравитации, с. 79. М., Наука, 1969]. Или так: “в
свободно падающей системе отсчета нельзя
наблюдать ни инерциальных ускорений, ни
ускорений тяготения (гравитационных ускорений)”
[там же, с. 78]. Или еще так: “Для
изучения солнечной системы никто не станет
использовать координатную систему, покоящуюся
относительно Земли, поскольку это непрактично. В
принципе же такая система, согласно общей
теории относительности, совершено равноправна
со всеми другими. Тот факт, что неподвижные
звезды будут двигаться с громадными скоростями,
если в основу исследования положить такую
систему координат, равно как и сложная структура
существующего в этой системе гравитационного
поля, имеющего, например, соответствующие
центробежным силам компоненты, представляют
собой возражения не против допустимости, а
только против целесообразности такого выбора
координат” [А. Эйнштейн. Диалог по поводу
возражений против теории относительности, собр.
соч., т. 1, с. 624, М., Наука, 1965].
Иными словами, их не волнует
переход между инерциальными и неинерциальными
системами отсчета. Они вполне могут оперировать
только неинерциальными системами отсчета,
придавая им некоторые взаимные постоянные
скорости, как они делали с инерциальными
системами отсчета. “Эйнштейн
высказался за отказ от любых попыток
восстановить прежнюю роль инерциальных систем
отсчета. Локально их роль должна быть передана
свободно падающим системам отсчета; однако эти
системы нельзя неограниченно продолжать” [П.
Бергман. Загадка гравитации, с. 79. М., Наука, 1969]
(добавим: чтобы не попасть в область
неоднородного поля, в котором законы сохранения
не справедливы). И для реализации этой цели
достаточно, чтобы законы выполнялись в самих
неинерциальных системах отсчета и чтобы это были
те же самые законы сохранения, на которых
построена механика в инерциальных системах
отсчета. При этом, как я уже сказал в начале
дискуссии, они получают право перетащить
преобразования Лоренца из инерциальной системы
отсчета в неинерциальную. |
Титульная
страница: /1 / 2 /
3 / 4 / 5 /
|
|







