СЕЛФ |
|
| Взаимоотношение углов в релятивистской концепции | |
|
|
СЕЛФ |
|
| Взаимоотношение углов в релятивистской концепции | |
|
|
Взаимоотношение углов во взаимно движущихся системах отсчета с точки зрения релятивистской концепции С.Б. Каравашкин, О.Н. Каравашкина Украина, 61140, Харьков, проспект Гагарина, 38, кв.187 Тел.: (057) 7370624 e-mail: selftrans@yandex.ru, selflab@mail.ru При представлении решения задачи о преобразованиях координат путем введения промежуточных систем отсчета мы могли убедиться, что различные пути приводят к различным решениям, что не характерно для евклидовых пространств. В качестве одной из предполагаемых причин подобного несоответствия релятивисты обычно приводят искажение углов при преобразованиях или поворотах осей на мнимый угол. Вместе с тем, как известно, одним из условий постановки Эйнштейном задачи нахождения преобразований Лоренца является именно параллельность координат: “Пусть теперь началу координат одной из этих систем (k) сообщается (постоянная) скорость v в направлении возрастающих значений x другой, покоящейся системы (K); эта скорость передается также координатным осям, а также соответствующим масштабам и часам. Тогда каждому моменту времени t покоящейся системы (K) соответствует определенное положение осей движущейся системы, и мы из соображений симметрии вправе допустить, что движение системы k может быть таким, что оси движущейся системы в момент t (через t всегда будет обозначаться время покоящейся системы) будут параллельны осям покоящейся системы” [А. Эйнштейн, К электродинамике движущихся тел, т.1, с. 13]. На данной обусловленности взаимной параллельности осей Эйнштейн основывает исходные уравнения преобразований в общем виде, которые в ходе его вывода приобретают форму преобразований Лоренца: “Можно выбрать обе системы координат так, чтобы ось x системы S и ось x' системы S' совпадали и чтобы отнесенная к S ось y' системы S' была параллельна оси y системы S … Из известного теперь положения координатных плоскостей системы S' относительно S непосредственно вытекает, что каждые из последующих уравнений попарно эквивалентны: |
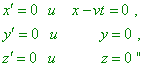 |
(1) |
[А. Эйнштейн, О принципе относительности и его следствиях, т. 1, с. 71]. Как мы можем видеть из цитаты, система уравнений (1) записана именно для параллельности осей взаимно движущихся систем отсчета и никаких поворотов не предполагает, как не учитывает и не предполагает преобразований в криволинейных пространствах. Также неосновательны ссылки релятивистов на повороты при преобразованиях. Подобные повороты в линейных пространствах задаются принципиально отличными от (1) выражениями, а пространство СТО по условию, введенному Эйнштейном, строго линейно: “Можно сразу сказать, что эти уравнения должны быть линейными по отношению к указанным переменным, поскольку этого требуют свойства однородности пространства и времени” [А. Эйнштейн, О принципе относительности и его следствиях, т. 1, с. 71]. Из этой же линейности следует и то, что трехмерное пространство СТО (пространственные оси) является евклидовым: “Равенство нулю тензора кривизны в евклидовом пространстве очевидно. Однако уже Риман в своей диссертации указал, что верна и обратная теорема: если тензор кривизны равен нулю, то пространство – евклидово, т.е. тогда можно найти такую систему координат, в которой gik постоянны. Впервые обстоятельное доказательство этого утверждения дал Липшиц. Очень изящное и наглядное рассуждение было проведено Вейлем” [В. Паули, Теория относительности, с. 78]. Таким образом ни о нелинейности пространства, ни о преднамеренных поворотах осей в теореме Эйнштейна говорить не приходится, а значит, в обоих вариантах, представленных в тексте решения задачи, все оси основных и вспомогательных систем отсчета сохраняют свою взаимную параллельность и в обоих случаях преобразование происходит из одной и той же системы отсчета S1 в ту же самую систему отсчета S2 . Тем не менее, чтобы снять излишние возражения релятивистов, рассмотрим закономерность преобразования углов во взаимно движущихся системах отсчета. При этом сразу обратим внимание на тот факт, что мы в данном случае не можем воспользоваться стандартной релятивистской формулой трансформации углов [В. Паули, Теория относительности, с. 32]: |
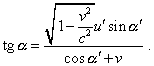 |
(2) |
Данное выражение записано для преобразования угла наклона скорости при переходе из неподвижной (нештрихованной) системы отсчета в подвижную (штрихованную). Именно в связи с этим в правой части (2) фигурирует не только взаимная скорость систем отсчета v , но и скорость тела u' относительно подвижной системы отсчета. А это в релятивистском формализме означает, что для неподвижных относительно подвижной системы отсчета тел формула (2) теряет смысл и для преобразования пространственных углов нужно использовать иную зависимость, выведенную именно для преобразования углов вектора, неподвижного относительно подвижной системы отсчета. Отметим здесь, что в классической физике данное различие абсурдно, но в рамках ее формализма не происходит и трансформации пространства-времени, как и сохраняется соответствие между углами наклона векторов во всех инерциальных системах отсчета. В релятивизме это условие преднамеренно нарушено, поэтому и закономерности трансформации углов необходимо искать для векторов скорости отдельно и для пространственных векторов отдельно, и как мы увидим дальше, данные зависимости принципиально различны. Чтобы найти закономерность
трансформации пространственных углов при
переходе из одной инерциальной системы отсчета в
другую в рамках релятивистской концепции,
рассмотрим две инерциальные системы отсчета K
и K' , из которых последняя движется в
направлении положительных значений оси x
системы отсчета K с сохранением полного
совпадения осей x и x' . Пусть также в
системе отсчета K' находится
пространственный вектор
|
Рис. 1. Схема движения
пространственного вектора
|
Чтобы корректно произвести расчет искомой зависимости углов, мы должны, в отличие от классического формализма, учитывать не только пространственные, но и временные характеристики, поскольку, как показано нами в работах , преобразования Лоренца наклоняют плоскость событий, вследствие чего появляется мнимая неодновременность. И если мы предполагаем, что угол наклона пространственного вектора производится в физическом времени каждой системы отсчета (что соответствует условию вывода Эйнштейном преобразований Лоренца), то мы должны производить дополнительные преобразования, чтобы согласовать результаты преобразований с физическим временем в каждой системе отсчета. С учетом вышеописанного, чтобы
преобразовать вектор для начала вектора x'1 = 0 , y'1= 0 , t' = t'0 и |
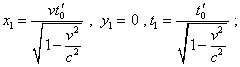 |
(3) |
для конца вектора x'2
= N' cos |
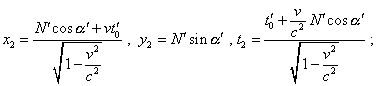 |
(4) |
Из (3) и (4) мы видим, что значение начала и конца вектора в неподвижной системе отсчета, как и ожидалось, отображаются в различные моменты времени. Чтобы ввести в соответствие полученные значения с физическим временем в неподвижной системе отсчета, достаточно учесть, что все точки, соответствующие этому пространственному вектору, равномерно смещаются во времени вдоль оси x системы отсчета K . Поэтому если положение начала вектора (x1, y1) соответствует времени t1 , то в этот момент времени конец вектора находился в точке с x-проекцией |
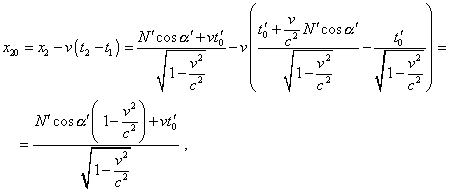 |
(5) |
y-проекция конца вектора при этом соответствует (4), поскольку смещение происходит вдоль оси x . С учетом (5) и (3), разность x-проекций в неподвижной системе отсчета равна |
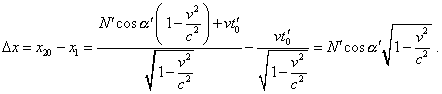 |
(6) |
Из (3) и (4) имеем для y-проекций |
| (7) |
Следовательно, |
| (8) |
Полученное выражение (8) описывает искомую нами зависимость, связывающую углы наклона пространственного вектора во взаимно движущихся инерциальных системах отсчета в релятивистской концепции. Сравнивая это выражение с законом трансформации векторов скорости (2), мы видим принципиальное отличие в самом характере зависимости. Это свидетельствует о том, что вектора различной природы в релятивистской концепции преобразуются различным образом. В связи с этим релятивисты не имеют права отождествлять законы преобразования векторов различной природы: "В общем случае четырехмерным вектором или, кратко, 4-вектором мы назовем вектор аа , имеющий проекции на оси координат аx , аy , аz и аt , которые при преобразованиях Лоренца - повороте осей в четырехмерном пространстве - преобразуются по одному и тому же закону. Именно компоненты любого вектора аа должны изменяться так же, как компоненты радиуса-вектора rа" [В.Г. Левич, Курс теоретической физики, т. 1, с. 217]. Далее, из (8) мы видим, что углы
наклона пространственных векторов, направленных
вдоль осей подвижной системы отсчета, не
трансформируются, т.е. при |