| Volume 4 (1999), No 4, pp. 5-13 | 5 |
| Solutions for finite elastic lumped lines | |
|
|
NATIONAL ACADEMY OF SCIENCES OF BELARUS STATE COMMITTEE ON SCIENCE AND TECHNOLOGIES OF REPUBLIC OF BELARUS ASSOTIATION “NOMATECH” INSTITUTE OF RESOURCE SAVING PROBLEMS V.A.BELYI METAL-POLYMER RESEARCH INSTITUTE OF NASB
MATERIALS. TECHNOLOGIES. TOOLS 1999, #4, pp. 5-13 |
|
|
|
MECHANICS OF STRESSEDLY-DEFORMED STATE |
|
|
|
| Exact analytical solution for 1D
elastic homogeneous finite lumped line vibration
S.B. Karavashkin Special Laboratory for Fundamental Elaboration SELF e-mail: selftrans@yandex.ru, selflab@mail.ru
Abstract We will analyse the main shortcomings of conventional approaches to the problem of vibrant 1D homogeneous finite lumped line and present the exact analytical solutions for forced and free vibrations in finite lines with the free ends and with the free end and fixed start. We will analyse these solutions and their distinctions from the conventional concept on the vibration pattern in such lines. We will give the check of presented solutions proving them to be complete and exact. Keywords: mathematical physics, wave physics, dynamics, finite elastic lumped lines, ODE systems, microwave vibrations in elastic lines Classification by MSC 2000: 30E25; 70E55; 70J35; 70J60; 70K40; 70F40 Classification by PASC 2001: 02.60.Lj; 05.10.-a; 05.45.-a; 45.30.+s; 46.15.-x; 46.25.Cc; 46.40.-f; 46.40.Fr
1. Introduction In [1] we studied the exact analytical solutions for infinite 1D elastic lumped lines and showed that in distinct from conventional solutions, the exact analytical solutions have generally three vibration regimes: periodical, aperiodical and critical. With it the vibration pattern essentially changes dependently on the line type (semi-finite or infinite) and on the vibration conditions, i.e., are they forced or free. Generally, finite lines have the same distinctions, but some others are inherent in them, also. In this paper we will study these features. 2. The drawbacks of conventional methods Two basic approaches are currently applied to find exact solutions for vibrations in 1D finite elastic lumped lines. They are the allowed modes method (see, e.g., [2]) and Krylov method (see, e.g., [3], [4] or [5]). To see their drawbacks, analyse each briefly. |
|
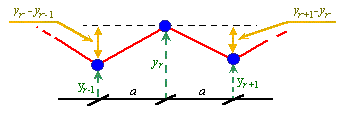
Fig. 1. The conventional model to calculate transverse vibrations in a finite lumped line
|
|
| In the allowed modes method the standard system of equations | |
|
(1) |
is taken as the basis, and yr means here the vertical shift of the elastic line, T is the line tension, m is the mass of a line element and a is the between-element distance in the line. We will study it after Pain [2] in relation to the transverse vibrations (see Fig. 1); for those longitudinal this technique is same. The solution of this system of equations is sought in the following form: |
|
|
(2) |
(where Ar is the amplitude of
line vibrations and |
|
|
(3) |
Substituting yr to the initial system (1), we yield a system of algebraic equations of a following type: |
|
|
(4) |
which can be naturally presented as the system of ratios
constant for the given line parameters and frequency |
|
is the circular frequency of affecting force), with the
following boundary conditions for a fixed-ends finite line:
