Materials.Technologies.Tools |
10 |
| S.B. Karavashkin | |
|
|
Thus, we see that the exact analytical solutions (32) essentially differ from the conventional solutions. As before, we can easy check that the expressions (32) really are the solutions, substituting them directly into the first, ith and last equations of the modelling system (29). For the left part of the first equation |
|
|
(35) |
and for that right |
|
|
|
|
|
|
|
|
(36) |
For the left part of the ith equation |
|
|
(37) |
and for that right |
|
|
|
|
|
|
(38) |
For the left part of the last equation |
|
|
(39) |
and for the right one |
|
|
|
|
(40) |
Proceeding from the described above and noting the theorem of uniqueness of a solution of differential equation, we can surely say that the presented solutions are exact, which substantially changes the concept of vibration processes pattern in finite lines. The same as in infinite lines considered in [1], the solutions transform with the line features, but remaining the block structure of solution. We can make it sure, considering a finite line having an unfixed start and fixed end. |
|
Fig. 5. Mechanical model of a finite lumped line with unfixed start and rigidly fixed end
|
|
3.3. The forced and free vibrations of an elastic line having unfixed start and fixed end In Fig. 5 we see the model of an elastic line with unfixed end affected by an external harmonic force F(t) . The following system of differential equations corresponds to this model: |
|
|
(41) |
Three solutions correspond to this system: for the periodical regime at |
|
|
(42) |
The vibration diagram for the periodical regime is presented in Fig. 6. |
|
Fig. 6. Vibration diagram for the periodical regime (m = 0,01 kg; s = 100 N/m; a = 0,01 m; n = 8; F0 = 0,6 N, f = 15 Hz) |
|


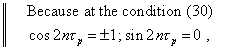 consequently,
consequently,






