Volume 4 (1999), No 3, pp. 15-23 |
19 |
| Exact analytic solution for 1D infinite vibrant elastic lumped line | |
|
|
Volume 4 (1999), No 3, pp. 15-23 |
19 |
| Exact analytic solution for 1D infinite vibrant elastic lumped line | |
|
|
Check, how these solutions satisfy the modelling system. It is sufficient to check them for the kth and the arbitrary ith equations of (23). Substitute the periodical solution (24) into the kth equation of (23). For the left side we yield |
| (26) |
for the right side |
 |
(27) |
This means, (24) satisfies the kth equation of system. Now substitute (24) into the ith equation. On the left side we yield |
| (28) |
and on the right one |
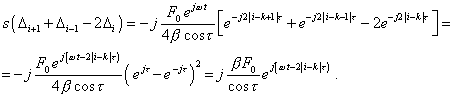 |
(29) |
Thus, the periodical solution satisfies (23) completely. Now check the aperiodical solution (25). For the left side of the kth equation we yield |
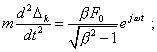 |
(30) |
for that right |
 |
(31) |
Finally, for the left side of ith equation: |
 |
(32) |
and for the right one |
 |
(33) |
As we see, solutions (24) and (25) satisfy the modelling system (23) completely. But, as it was pointed before, by contrast to the solutions for semi-finite line, the given model has not a final solution for the critical regime. And this is easy to prove by checking the completeness of the amount of solutions (24)–(25). According to the above conditions of critical
regime, it is an intermediate between those periodical and aperiodical; consequently, if
in the aperiodical solution we direct |
| (34) |
i.e. the solutions (24)–(25) are same complete as (6)–(8) are. At the same time we see that the aperiodical
solution easily transforms into the critical one; we can prove it also for the relation
between the periodical and aperiodical regimes. Basically, all three yielded solutions are
three forms of one solution transforming in accordance with the value |