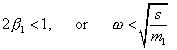V.2 No 1

67

On solution for an infinite heteroheneous line

4.3. m₂ =

With the same principle we can yield the solution for a semi-finite line with a fixed end. We should note that when the masses m₂   turned to the infinity, vibrations in the section containing these masses turn into the periodical regime. Besides, it follows from this condition that at m₂ 

To transform (2)–(4), conveniently use the system (11)–(13) where we took into account the transition of the third section vibrations into aperiodical regime. Sequentially substituting (33) to the expressions of this system, yield:

for i k

for k i n

and for i n + 1

In the first section, there propagates the progressive wave whose amplitude depends in a complex way on the external force frequency and the line parameters. In the second section the standing wave with some phase delay 2(n – k)₁   has formed. In the third one, just as it was expected, the vibration amplitude is zero.

If we continue transforming the solutions (34)–(36), taking k = n , we will yield the solution for a semi-finite elastic line whose first element after fixation the external force affects. With it only one solution of three will remain:

Comparing (37) with (32), we see that at the same external force parameters, the vibration amplitude in a line with fixed ends is less at low frequencies, when the condition

is true. At the frequencies higher than indicated in (38), the vibration amplitude in the line with a fixed end will be higher than in a line with unfixed end.

Thus we see that the basic solutions are easily transformed into solutions for the models covered by the basic model. This is a very important property of the complete analytical solutions. Should the initial basic solutions be incomplete, or should they be presented only numerically, such transformation would be impossible.

5. The limit passing to a distributed line

To make our analysis complete, trace the transformation of solutions (2)–(4) at the limit passing to the distributed line. To transform the basic solutions for this case, present the parameters of elastic line in the form corresponding to that lumped. To do so, introduce

where T is the stiffness of lumped line, a   is the distance between unexcited elements in a lumped line, and ₀₁ , ₀₂   are the densities of related sections of heterogeneous unexcited lumped line.