V.2 No 1

69

On solution for an infinite heteroheneous line

In the first section there propagates the progressive wave whose phase shift is determined by the complex multiplier in the square brackets of (42):

In the second section we see a complex vibration process determined by the similar expression in brackets in (43). On one hand, the wave process in this section has the phase

depending on x₀  nonlinearly. On the other hand, the wave amplitude depends on this parameter nonlinearly, too. Its quantity is proportional to

The amplitude will reach its extreme values at the points

where p = 0, 1, 2, ...  . In the first case (47) is equal to v₂ , and in the second case – to v₁ . Depending on the relationship in the wave propagation velocities in related sections, the maxima and minima of the wave process will be seen at these points.

The results yielded for the first and second sections much differ from the conventional understanding based on a simple superposition of the direct and reverse waves. According to this understanding, “the amplitude reflection coefficient

the amplitude transmission coefficient

(where A₁, A₂, B₁ are respectively the amplitude coefficients of direct, reflected and transmitted waves; Z₁ = ₀₁₁ =T / ₁  is the mechanical impedance of the first section of an elastic line; Z₂ = ₀₂v₂ = T / v₂  is the mechanical impedance of the second section of an elastic line – Authors). These coefficients do not depend on and are same for waves of any frequency. They are real and do not introduce any phase shifts except the shift by changing the sign of the term” [11, p. 123].

As we see from this analysis, when reflecting from the heterogeneity transition, there forms a complex wave process whose phase and amplitude depend directly on the external force frequency, the same as on elastic line parameters. These conclusions are true also for the transmitted wave.

In the third section of elastic line we see the progressive wave having the along-line phase delayx₀ / v₂ and common phase shift determined in (44) by the unit imaginary number and  x_k / ₁ .

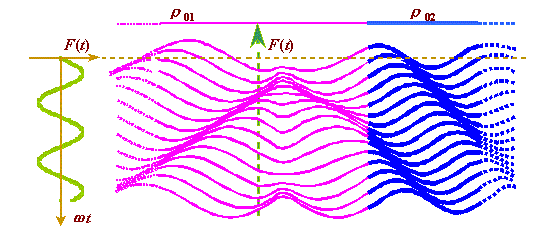
Fig. 4. The diagram of transverse vibrations in a heterogeneous elastic distributed line with the frequency f = 5 Hz and amplitude F₀ = 1 N . The line parameters: ₀₁ = 1,7 kg / m ; ₀₁ = 4,5 kg / m; T = 1 N

To see the typical vibration pattern, conveniently pass from the longitudinal to transverse vibrations. It will be sufficient to direct the external force perpendicularly to the axis of line and substitute in the solutions (42)–(44) the longitudinal shift x - x₀ by that transverse y . The typical diagram of transverse vibrations in a heterogeneous distributed elastic line is shown in Fig.4. The pattern presented in it fully corroborates the above analysis of solutions (42)–(44).