4

S.B. Karavashkin and O.N. Karavashkina

To make the analysis of (11) easier and more visual, plot the space-time diagram of the vector (x, t)   amplitude variation, beginning from some arbitrary chosen initial time t₀ , as we did it in [10]. The general form of this diagram is shown in the centre of Fig. 2. As is usual for delaying processes, the phase of vector (x, t) oscillations displaces with growing x . Different parts of the wave appear in the domain of paths picked out being well-visible due to the dotted lines dropped from the sides of paths to the diagram. Therefore at the opposite sides of paths there are indicated the different values of the momentary amplitude of the vector (x, t) . It evidences that the circulation of the vector (x, t)  is non-identical to zero. We can easy calculate this circulation of the vector, noting that the wave front is plane and the flux is 1D. Due to it, the integration in the expression (11) reduces to a summation of scalar products of the momentary values of vector (x, t) amplitude by the length l of corresponding sides of the chosen path.

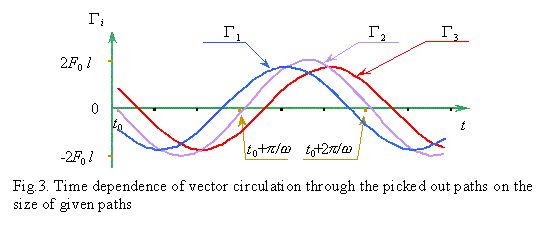
The results yielded for each of chosen paths at the instances shown in Fig. 2 (left) are shown in Fig. 2 (right).

The calculations show that, actually, the circulation _i  is not identically zero. Its value varies in time and does not coincide for all three picked out paths. It is graphical in the plot _i(t) shown in Fig. 3. We see that both the amplitude and phase of oscillations of the circulation of vector in time depend on the paths size.

We can write it as follows:

where x_i = x_i - x₀   ; i = 1, 2, 3.

As _i ( x_i)  appeared because of finite velocity of a wave space-propagation, we can express  x_i   through the time delay characteristic of wave:

where t_i  is the delay time, with the wave passing between the opposite sides of the ith path picked out.

Substituting (13) into (12), we yield

Noting that the square size of the path picked out depends on  x_i   too as

It means, the curl of vector also will not vanish:

We see from (17) that the value of curl of vector (x, t) in case of dynamical field depends on the frequency of field variation and on the wave propagation velocity, and the phase of curl variation leads the phase of vector oscillations by  /2 . When passing to the stationary fields, i.e. at 0 and/or c , the right part of expression (17) automatically vanishes, agreeing with the conventional concept (2).

With all simplicity of this derivation and obvious result, we note that when transiting to the stationary field, the curl of vector vanishes. It can be easy generalised for the case of arbitrary flux of vector.