curl05

V.2 No 2	5
Theorem of curl of a potential vector

3. Complete proof of curl of vector theorem for dynamical fields Consider some dynamical flux of the vector (, t) going through a picked out connective region V free of vortexes and currents (see Fig. 4). With it we will suppose that the direction of vector (, t) is perpendicular to the flux direction .

Limit the picked out region V from the sides - by the lines of force, and from the ends - by the equiphase surfaces of flux. Then all lines of force going through V will have equal lengths, and the following relation between the length of line of force l and the time delay t is true:
	(18)
Introduce the co-ordinate system (n_r ; n_n; n_b) in which _r is directed with the flux direction , _n is directed along (, t), and _b is binormal to _r . Pick out in the region V the surface ABDE whose sides AB and DE belong to the ends of region V, and the sides AE and BD coincide with the lateral surface of the picked out region and are parallel to _r . In the introduced co-ordinate system, (, t) can be presented as
	(19)
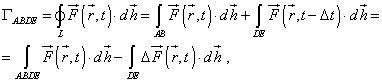Using the conventional definition (9) and taking into account that at a distant end of the picked out region V the phase of vector oscillations delays by some time interval t, we can determine the circulation _ABDE of the vector (, t) as
	(20)
where d is an infinitesimal element of the length of segments AB and DE of closed path L, and

As we see from (20), due to the appeared phase delay, the circulation of vector divides into two parts: the conventional spatial circulation of vector and the integral depending on the spatial wave delay. The first part, in the absence of vortexes and currents, naturally vanishes. The second integral around the closed path L easy transforms into an integral about the surface S bounded by this path. To make this transformation, divide the surface S into p surfaces along the flux propagation. Then (, t) can be presented as
	(21)
where


and 1 i p in this case. Passing to the limit at t 0, we yield
	(22)
Substituting (22) into (20), we yield
	(23)