SELF

14

S.B. Karavashkin and O.N. Karavashkina

2. Comparison of experimental results

For this aim, we have used the well-analysed experimental results on the investigation of the near EM field at a long-wave band, as described in the survey monograph by the team of authors led by Ya.L. Alpert [18, p. 836- 845]. In the Chapter VI, "The radio waves velocity", they study the regularity of variation of the additional phase  *  in the near field of the source of transverse EM waves. As the authors conclude, "… the formula of vertical component of the electric field of dipole … , noting the phase of wave, has the following form:

where  E _z is the vertical component of the electric field of dipole;

W  is the source power in kilowatts;

 f() is the module and    is the phase of the attenuation function   f() ;

is the wavelength;

is the dielectric constant of the Earth surface. However, (19) is true only at the distances  r (4 5)  from the radiator" [18, p. 837]. In other words, only in the region exceeding five lengths from the radiator we can think true the assumption that the long waves propagate in the wave guide layer between the Earth surface and ionosphere, on whose basis (19) has been obtained.

"But the phase structure of electromagnetic field and the velocity of radio waves have … some features just at nearer distances immediately bordering on the antenna. In this region we have to use for calculations more complex formula having the following form [19]:

where k₂ =  k₁(')^1/2 =  k₁[ - i(4/)]^1/2 and is the electric conductance of the Earth. The values f() and    are calculated in a complex way with the help of series" [18, p. 837]. "The above formulas relate to the case of vertical dipole placed on the Earth surface. In approach to the radiation point, at distances  r 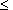  the finite size of the antenna begins to have an effect. So (20) becomes invalid for exact calculations of the field structure. There are no rigorous formulas of electromagnetic field that take into account both the finite size of antenna and finite conductance of the Earth. However the field structure analysis showed that at these distances the formulas derived for the case when the conductance of the Earth is taken infinite are quite valid. In this case the phase _z  of vertical component E   is determined as

[18, p. 838- 839], where R₁ ,  R₂ , R₀ is the distance to the top, bottom and mirror ends of antenna correspondingly, and ₀  is so-called shortening of antenna meaning the section adding the length of antenna to  /4 .

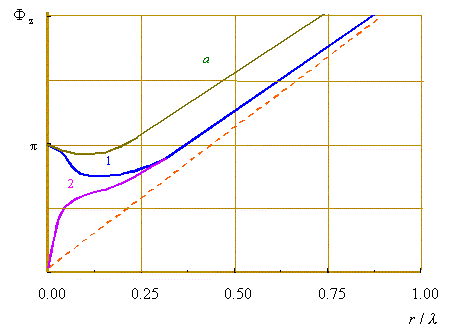
Fig. 3.  Theoretical dependence of phase _z wish respect r/ to in the near of antenna: 1 is the antenna with the lebhthing at   = , 2 is antenna with the shortening at = , a is vertical dipole at = 1,7*10⁶ CGSE , = 4. [17, p. 840, Fig. 122.4]

"The curves of regularity _z with respect to r/ constructed on the basis of (21) for different values ₀ (see Fig. 3) illustrate the details of variation of the wave phase near the antenna; for comparison, in the same figure we show the curve _z  calculated by (20) for = 1,7*10⁶ CGSE and  = 4 " [18, p. 839].

We see from this plot that the curves calculated by both above formulas predict the end of near field in limits  r = , though, as the authors said, the region of near field is much larger. Another drawback of these curves is the bad correlation between the curves a and 2, while a well correlates with 1 immediately near the radiator. None the less, the data of plot show that in the near field of EM radiator the phase is not constant, as implied in the absence of travelling wave in this region. This additionally evidences that it would be incorrect to neglect the delay phase in the near field, as we indicated it in [11].