V.4 No 1

5

On gradient of potential function

In this view we can consider the model of field of pulsing source as a system of equipotential lines with decreasing amplitude of potential with the distance from source which propagate from the source with velocity  c. With it the equipotential line radiated by the source at some moment  t₀   will reach the studied point  P₀ located at the distance r from the source during the time

(see Fig. 3), and point P₁   located at the distance  r  from P₀ - during the time

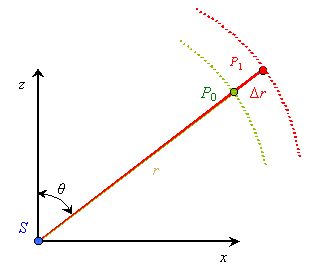Fig. 3. Equipotential lines of pulsing point source

So, if we now want to determine the derivative of scalar potential along the direction from the field source, we will see that at the points P₀ and P₁ there are the potentials radiated by the source with the time interval t . In this connection, the derivative along the radius-vector will have the following form:

As we can see from (10), the dynamic gradient (which we wrote down with the capital letter, in order to distinguish it from the gradient of function with respect to coordinates) consists of two summands. The first summand is a known gradient for stationary fields, and the second summand accounts the time variation of gradient of potential due to dynamic pattern of the field.

But this second summand is just the time-dependent summand in (1). And we can mark the feature of limit passing from the increment of function to the time derivative in second summand. Despite in second equality of derivation (10) we take the difference of potentials radiated at the moment (t -  t)  minus that at the moment (t) , none the less in the next equality the sign before the second summand will not change, though  t  is negative. This is like determining the signal delay phase by the screen of oscillograph. On one hand, in finding the derivative with respect of radius-vector we have to take in general case the difference between the far and near points of the field, but the first of subtracted potentials has been radiated by the source before the second. Just this makes the sign unchanged when calculating the derivative, despite the negative time increment.