SELF |
48 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
48 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
3. Classical and relativistic solutions of Doppler effect in comparison of their approaches To compare, write general Doppler solution in the relativistic formalism [2, p. 36, formula (15)]: |
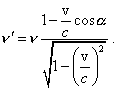 |
(11) |
Comparing (11) with (9), we see that generally formulas
are mutually irrelevant both in the form of mathematical regularity and in the amount of
parameters on which the frequency shift depends. In classical formula, the shift depends
not only on the angle In Fig. 3 we show the regularities of signal frequency
received by the moving observer, with respect to the angle |
|
Fig. 4. Frequency of signal received by the moving
observer, against the angle
|
We see from the plot that Doppler shift predicted by
relativistic conception is much higher than the values predicted by the classical
conception. And at And, as we told above, the classical solution depends on
many parameters, not only on ratio of observer's speed to that of light. In Fig. 5 we show
the regularities of frequency of signal received by observer against the angle |
|
Fig. 4. The frequency of signal received by moving
observer against the angle
|
The plots show, the transverse Doppler effect in the view of classical formalism is revealed at small aimed distances and grows with their fall. But the effect always gives negative values of frequency shift. It is important to mark here that as relativists state the problem, with lessening mutual speed of observer and source, all effects predicted by their conception have to be reduced to those classical. Should the predictions of classical conception were different only in sign, relativists could operate, neglecting the quadratic terms at small speeds. But factually the point is much deeper, as the sign of effect cannot be negated by disregarding of quadratic terms. This clearly speaks of erroneous premises on which the relativistic conception has been formulated, and below it will find additional basic corroboration. To deepen the comparison, consider particular cases of longitudinal and transverse Doppler effect. |
Contents: / 46 / 47 / 48 / 49 / 50 / 51 / 52 / 53 / 54 / 55 / 56 /