|
v.7 No
1 |
1 |
| On conservation of energy
and impulse |

|
On conservation of energy and
impulse
VLADIMIR: Something is unclear in the page 73 of your paper “The problems
of physical time in today physics”. Not exact understandable, of which conservation
of impulse and energy are you speaking in case of resting reference frame S? The
set of particles in the outer field is not closed-loop and they move with acceleration?
Unclear.
SERGEY: As we showed from the view of classical mechanics,
in the homogeneous field, the conservation laws ‘pass’ from the non-inertial
frame to that inertial, because the acceleration of the very frame is identical to the
acceleration of material bodies.
VLADIMIR: I would like to draw your attention that
the very your phrase (I’m citing) “Thus, if in one frame
the law of impulse conservation |
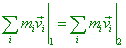 |
(6.38)(d1.1) |
is true, where 1 and 2 denote the sum of
impulses before and after some process occurring in this frame, then in the another frame,
according to (6.36), the equality (6.38) will be true, too” – has no place in classical physics,
as all conservation laws it formulates for one (resting) inertial frame. Then, if we want
to consider the same frame from another IRF, neither impulse nor kinetic energy of the
frame will remain same – on the contrary, they will change, and classical physics
points, how they change.
SERGEY: You are saying right, dear Vladimir, but tell me
please, if in one IRF the conservation laws for energy and impulse remain true, do they
remain true in another frame? From the view of classical physics, of course. 
VLADIMIR: From the view of classical physics, in all IRFs
the conservation laws for energy and impulse work, indeed. But the energy and impulse do
not conserve in passing from one IRF to another.
SERGEY: In frame-to-frame translation, the numerical
values of energy and impulse will naturally change. And I can mark, relativists will agree
with the fact of this change. But the conservation laws are written not for frame-to-frame
translations but as the conservation of impulse or energy in some interactions within a
set of material bodies in this frame. Is not it so? This is why I asked you: in one frame,
when some interaction within the set of material bodies, the conservation law is true.
Will it be true if we observe this interaction from other frame that moves inertially? Is
not it just what you mean, saying, “The conservation laws of energy and impulse
work”? 
VLADIMIR: From the view of classical physics, the
conservation laws for closed-loop systems have to be true, when we observe from any IRF.
For different IRFs, different constants responsible for the motion of mass centre of the
system are added.
SERGEY: Yes, indeed, the constants are different, and
relativists have different measures. But if the conservation laws are translated from one
frame to another, we see it so as it is shown in the formulas (6.34)–(6.45). This
means, we have an equality – for example, of the sum of impulses before and sum of
impulses after interaction. We pass from one frame to another and yield the equality of
same sums but with other values of speeds corresponding to other frame. And constants can
take place only when we consider just the sum of impulses of the set or the total energy
of set. When we equalise them, constants are deleted, aren’t they?
VLADIMIR: Then let us return to the statement of problem,
please.
Some region of space is given so that a homogeneous
gravity field affects it, and we have two reference frames: S is the inertial
(resting) frame and S' is the freely falling frame, and we have some compact set of
n masses mi , i = 1, 2, 3, … , n each of which
at the initial moment t0 has the speed v'i relative to the freely falling frame S'. As far as I can
understand, relative to the frame S the speed at the initial moment of time is
same.
Let us consider in frames of classical physics.
The formulas (6.34)–(6.37) are true. Untrue is the
statement following them: “Thus,
if in one frame the law of impulse conservation (6.38) is true, where 1 and 2 denote the
sum of impulses before and after some process occurring in this frame, then in the another
frame, according to (6.36), the equality (6.38) will be true, too”. I already wrote you of it. Why? Because in the
accompanying frame S', all n masses mi are under affection
of no force (the resultant of gravity and inertia force is zero). While in the frame S
all masses are affected by the non-compensated gravity force, so the frames are basically
different. In one of them, S', the set of masses can be considered as the
closed-loop system, and the conservation laws for energy and impulse will be true in it.
In another frame, S, the same ensemble of masses cannot be thought as the
closed-loop system and the conservation laws for impulse and energy of the system will be
untrue in it.
And (6.36) has no concern here. Or rather, just (6.36)
says that if (6.39) exists, (6.38) can be true in no way. Clearly, if the moment of time 1
is initial t0 and at this moment v and v’ coincided,
then at the moment of time 2, in the frame S, the systematic vrel
is added to the regular increments v’ (in the frame S’). Thus, the
relationship (6.38) which you state does not exist and is impossible.
SERGEY: This is just the thing, dear Vladimir! The
derivation after (6.39) just shows, how namely the initial sum bifurcates into two
components. If in each expression the second sum does not depend on the processes inside
the system of material bodies (i.e., will not include the parameters related to the speeds
of these bodies and their location in space), in substitution of these expressions into
(6.38), the second sums will be cancelled. There will remain only the terms with
parameters in primed frame, and the equality will gain the same appearance but in other
parameters. In classical formalism this takes place in translation between IRFs (due to
which we say of equivalence of IRFs for laws of dynamics), and in translation between
inertial frames and frames freely falling in the homogeneous gravity field, of which
Einstein tried to make use. Only in these two cases the second sums will not involve the
speeds and coordinates of frames. Out of this, the equivalence will not be true.
VLADIMIR: I agree with “same appearance”, as the
expression for kinetic energy does not change its appearance in translations. But
the derivation after expression (6.39) is fully wrong, and I will explain, why.
You are stating: “Actually, let in the resting frame the energy conservation
law is true; then we may write (6.42)"; it follows from this that
left parts of (6.43) and (6.44) are equal.
First, the very statement started with the word
“let…” looks like beforehand untrue or impractical, as the increment of
kinetic energy of particles due to the acceleration in the gravity field cannot be
compensated within the closed-loop set of particles.
But even if we shut our eyes that the initial statement is
incorrect, we anyway will inevitably come to “Now, to yield
from (6.43) and (6.44) the energy equation for the moving frame, we only have to account
that the second summands in the right parts of these expressions are equal”.
No, aren’t equal, dear Sergey. Each summand (the
second summands in the right parts) in case 2 are more than the correspondent summand in
the sum ‘1’ by g?t where ?t is the difference between the
moments of time. Look again attentively. Finally, reject your marks of cases as
‘1’ and ‘2’ which disallows you to consider in details the
expressions, and you will see, you equalise unequal values.With it, your statement “and the third summands are equal, which follows from the
conservation of the impulse of system” is untrue, as the impulse is conserved
only relative to the frame S’, not to S.
To the point, I agree with (6.45). This expression is true
due to the conservation laws in the closed-loop frame. But why you came to the true (6.45)
through untrue (6.42)–(6.45) – I don’t understand.
SERGEY:
1. Let us, dear Vladimir, be not in hurry to seek the
incorrect. Sometimes it happens that we take the misunderstood as incorrect, true? For
example, above you stated that transition from (6.38) to (6.39) is incorrect. Now you
agree, in the impulse conservation law, the conservation law has to have same appearance
in each frame. But you did not lift the question of frame-to-frame translation in the
impulse conservation law, jumping to the energy conservation law.
2. At the same time, for same interaction, the
conservation laws to be same, all excessive relationships have to disappear (or appear) in
them, keeping the law same, true?? 
3. Let us finish with the question that you raised and
see, whether the translation is correct when we use the equations that we gave in support
of (6.39).
I would suggest returning to the scheme that we gave in
the first version of this work, where you truly corrected me. Having sorted this scheme
out, we just will catch, what is translated and why. Aren’t you against?
VLADIMIR:
1. See, dear Sergey, I never argued the form of
conservation laws, so I agreed. However, the form of laws is one thing but their
correctness is other.
2. No, not so. The form of law is, for example, “the
sum of impulses is constant”. ‘Excessive’ relationships in different frames
also have to give a constant, not to be cancelled. Then the laws are true or unchanged, as
you are saying. But we should not forget, the conservation laws ‘automatically’
are true only for closed-loop systems. While your set of particles is in the external
field, which means – just non-closed-loop. So I think that you should reconsider all
computations of (6.38)–(6.44).
3. I’m not against any form of consideration, if you
think, it will make our way to truth easier. |
SERGEY: Here we, dear Vladimir, approach the first
interesting point of our discussion. It follows from your second item that the
conservation laws are automatically true only for closed systems. And it outwardly
corroborates the existing definitions of conservation laws:
“Conservation laws are the physical
regularities according to which the numerical values of some physical values do not change
in time in any physical processes (sometimes in a definite class of processes)” [M.B. Mensky. Conservation laws. – In: Physical
encyclopedia, vol. 4, p. 591. Moscow, Soviet Encyclopaedia Publishing, 1965].
As we see, the definition also points the conservation of
numerical value in time, which premises the set of material bodies to be conservative,
too.
But this definition, as well as your statement, premises
that, if the system of material bodies is not closed, i.e. is not conservative, and is,
for example, in the field of external forces, the conservation laws in this system are not
true. Fine. Now, if you please, we will pass to our old problem, which we agreed to
consider.
You hopefully remember Fig. 1 in which we showed the model
of some body’s interaction with a massive wall; they both are in the external field
of gravitating body.
As you remember, the statement of problem and beginning of
calculation were the following.
Two reference frames are in some gravitating centre, one
of them is inertial and resting relative to the gravitating body, and the second (primed)
freely falls in the field of gravitating body. At some initial moment of time these frames
coincide; the initial speed of the freely falling frame is zero at this moment. In the
freely falling frame we have some body whose mass is m and a massive wall that at
the initial moment of time is at the distance L’ along the direction to the
gravitating centre, as is shown in Fig. 1.
|

Fig. 1. Interaction of some body A’ with the
massive wall in the external field of gravitating body
|
Let at the initial moment of time the material body gains
towards the wall some speed v'0 relative to the freely falling frame. Let us see to
which distance the studied body will jump (if absolutely elastic interaction) in the
freely falling frame during the time equal to the time of its flight to the wall. If
speaking of equivalence of laws in inertial and non-inertial frames, we first of all have
to make sure that at non-relativistic speeds in both frames, the conservation laws remain
true equally. The below calculation is targeted just to it.
We will calculate in the IRF and will follow at the same
time the trajectories of both studied body and of the point A’ of freely
falling frame from which the studied body started its motion, in order to compare the
location of the body and of the initial point.
Let us begin with the trajectory of material body. As it
has a mass, its motion relative to the IRF will be uniformly accelerated, which means,
uniform in relation to the freely falling frame. In the first section of trajectory, i.e.
when moving to the wall, the equations of motion, from the point of IRF, will be |
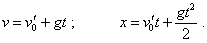 |
(d1.2) |
The body will reach the wall at the moment |
 |
(d1.3) |
With it, its speed from the point of freely falling frame
will remain initial, i.e. v'1 = v'0 , but from the point of resting frame, the speed of body,
with account of (d1.2) and (d1.3), will be |
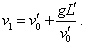 |
(d1.4) |
This event will occur at the point x'1
= L' of freely falling frame and at the related point |
 |
(d1.5) |
of IRF. In parallel with the body in IRF, the initial
point A’ will move. At the moment t1
it, together with the coordinate origin of freely falling frame, will have a
position |
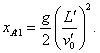 |
(d1.6) |
Now we have to calculate, how the studied body will be
reflected from the massive wall from the point of resting frame. Which laws have we to use
if the wall and the body move with uniform acceleration in the outer gravity field and
this set of material bodies is open from the point of resting frame?
VLADIMIR: To calculate “from the point of resting
frame”, we have to use the conservation laws when elastic collision of two bodies,
thinking the collision as the process having no duration.
SERGEY: Fine, dear Vladimir. But how about the common
statement that “Conservation laws are the physical regularities
according to which the numerical values of some physical values do not change in time in
any physical processes”? Does not it follow from it that the existing
interpretation does not encompass the whole set of laws? If there exist the conservation
laws which we can apply “as the process having no duration”, by definition and
in writing they have to differ from the conservation laws defining the conservatism of set
of material bodies, true?
VLADIMIR: Perfectly true, dear Sergey. But in the
formulation you gave, the author says of conservation of “some physical values”
of considered physical system in time; just the closed-loop system is of importance here,
interactions are another song. They are ambiguous in the meaning of conservation laws.
When different interactions, not all conservation laws can work. For example, inelastic
collision – the law of impulse conservation works, the law of energy conservation
– does not. In the model of elastic collision we premise losses of mechanical energy
absent, so conservation laws work both for impulse and energy.
I would like to say, each kind of interaction in the
meaning of conservation laws is considered separately, and the parameter of time is
accounted not always. In particular, in the model of collision we neglect it, considering
the balance of momentary values of impulses and energies ‘before’ and
‘after’.
SERGEY: Just in this meaning of balance of momentary
values of impulses and energies ‘before’ and ‘after’ we write the
expressions for impulse and energy in interactions within the set of n bodies that
raised your protest.
On the other hand, please draw your attention that,
speaking of fail of conservation laws, you are speaking of nonlinear processes – such
as an inelastic collision, – in which, even in limits of one inertial frame, the law
of impulse conservation also does not work and we have to introduce additional matching
coefficients determined, as a rule, experimentally and with quite large error, when it is
hard to distinct, which of ideal conceptions is true, the more that these competing
conceptions give alike values in the domain of achievable speeds and accelerations. While
for ideally elastic bodies, material points, ideal constraints – i.e., idealisations
with which classical theoretical mechanics operates, – we can surely state that in a
homogeneous gravity field in freely falling frame, the laws of conservatism are true, i.e.
the conservation laws for energy and impulse of motion of material point in time, and
conservation laws for energy and impulse in ideal interaction of bodies.
Another thing that interrelation between the inertial and
non-inertial frames does not retain, for example, the condition of conservatism, because
in gravity field in IRF, the total impulse and total energy will permanently change, while
in freely falling frame these parameters will remain constant.
But for relativists it is of no importance that the
parameters will not conserve in translation between inertial and non-inertial frames. See,
how they write: “The presence of gravity field causes such
phenomena in inertial reference frames which are locally indistinguishable from inertial
acceleration which we could see in non-inertial frame” [P. Bergmann. The
riddle of gravity, p. 79. Nauka, Moscow, 1969 (Russian)]. Or so: “in
the freely falling frame we can see neither inertial accelerations nor gravity
accelerations” [ibidem, p. 78]. Or one more so: “To
study the Sun system, no one will use the coordinate system resting relative to the Earth,
this is impractical. While basically, such system, according to general theory of
relativity, is absolutely equivalent to all others. The fact that stationary stars will
move with tremendous speeds if we base our study on such coordinate system, the same as
the complicated structure of gravity field existing in this system that has, e.g.,
components corresponding to the centrifugal forces give the arguments not against
admissibility but only against efficiency of such choice of coordinates” [A.
Einstein. Dialogue on objections against the theory of relativity. – In: Collections
of scientific works, vol. 1, p. 624. Nauka, Moscow, 1965 (Russian)].
In other words, they don’t care of translation
between inertial and non-inertial frames. They can operate enough only with non-inertial
frames, giving them some mutually constant speeds, as they did it with IRFs. “Einstein spoke against any attempts to restore the previous part of
inertial reference frames. Locally, their part has to be passed to the freely falling
frames; however, we may not unlimitedly continue these frames” [P. Bergmann.
The riddle of gravity, p. 79. Nauka, Moscow, 1969 (Russian)] (I would add: lest to appear
in the region of inhomogeneous field in which the conservation laws are invalid). And to
make these aims real, it is sufficient, the laws to be true in the very non-inertial
frames and they to be the same conservation laws on which the mechanics in IRFs is based.
And, as I already said in the beginning of our dialogue, they get a right to transfer the
Lorentz transforms from inertial frame to non-inertial. |
Title
page: /1 / 2 / 3 / 4 / 5
/
|
|







